Pendants
What proportion of each of these pendants will be made of gold?
Problem
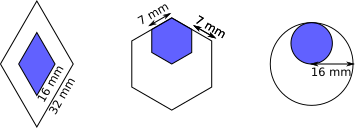
These designs are going to be made into pendants.
The diamond shape is a rhombus, the hexagon is regular, and the radius of the large circle is 16mm long.
For each pendant, the blue shape is a smaller version of the whole pendant.
What proportion of each pendant will be blue?
Image
Student Solutions
Using scale factors
Notice that, in each case, the side length (or radius/diameter) of the smaller shape is exactly half of the side length (or radius/diameter) of the larger shape. So the length scale factor in each case is $\frac{1}{2}$.
This means that the area scale factor between the larger shapes and the smaller shapes is $\frac{1}{4}$. So $\frac{1}{4}$ of each pendant will be blue.
Using shapes and areas
For the rhombus, either of these diagrams are helpful.
Image

Image

From the right-hand diagram, since the blue shape's sides are half the length of the large shape's sides, the yellow areas add up to the blue area, and the yellow area added to the blue area is equal to the sum of the red areas. So the blue area occupies $\frac{1}{4}$ of the total area.
From the left-hand diagram, the four small rhombi are all congruent, because they all have side length equal to half that of the larger rhombus. So the blue area occupies $\frac{1}{4}$ of the total area.
For the hexagon, part of a 'honeycomb' pattern is helpful.
Image
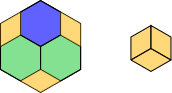
The two green hexagons are congruent to the blue hexagon, and notice that the three yellow pieces can be stuck together to make a fourth hexagon. So the blue area occupies $\frac{1}{4}$ of the total area.
For the circle, the area of the large circle is $\pi \times 16^2=256\pi$, and the area of the smaller circle is $\pi\times 8^2=64\pi$, which is $\frac{1}{4}$ of $256\pi$. So the blue area occupies $\frac{1}{4}$ of the total area.
