No rights
Prove that the angle bisectors of a triangle can never meet at right angles.
Problem
The angle bisectors are drawn onto a triangle.
Prove that the angle bisectors cannot meet at right angles.
Image
Student Solutions
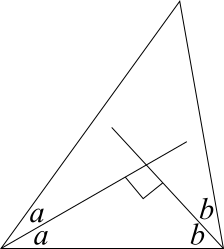
In the diagram, the two angles marked $a$ are equal, and the two angles marked $b$ are equal, because the lines are angle bisectors. They are shown crossing at $90^\circ$ to see what would happen if they did meet at a right angle.
Image
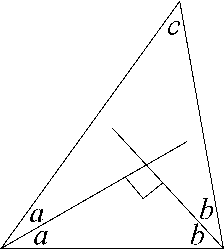
From the right-angled triangle inside the original triangle, $a+b+90=180$, so $a+b=90$.
If we let $c$ be the remaining angle in the original triangle, we have that $2a+2b+c=180$. However, since $a+b=90$, we must have $180+c=180$, so $c=0$, which doesn't make sense!
So if the angle bisectors cross at a right angle, then the triangle is impossible - so the angle bisectors can't ever cross at a right angle!
