Two equilateral triangles
Prove that these two lengths are equal.
Problem
The two black triangles are both equilateral, and their bases form a straight line segment.
Prove that the two red lines are of equal length.
Image

Student Solutions
Using rotation
Consider the coloured triangles in the diagram below. They both have one side equal in length to the larger equilateral triangle, and these sides are at an angle of 60$^\text{o}$ to each other. They also both have one side equal in length to the smaller equilateral triangle, and these sides are also at an angle of 60$^\text{o}$ to each other.
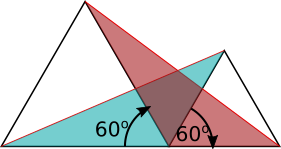
So a 60$^\text{o}$ rotation will map the blue triangle onto the red triangle. So the two triangles must be congruent. So the third sides, which are the red lengths, must be equal.
Using 'side angle side'
Let the sides of the larger equilateral triangle have length $a$ and the sides of the smaller equilateral triangle have length $b$, as labeled in the diagram. Notice that both the red triangle and the blue triangle contain an angle of 120$^\text{o}$ between sides of length $a$ and $b$.
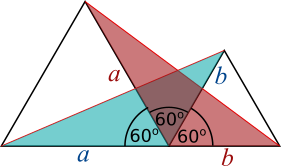
The lengths of the two sides and the size of the angle in between them uniquely define a triangle (imagine putting the ends of two sticks together at a fixed angle, joining the other ends of the sticks would complete the triangle). So the two triangles must be congruent, which means the third lengths must also be the same.
Consider the coloured triangles in the diagram below. They both have one side equal in length to the larger equilateral triangle, and these sides are at an angle of 60$^\text{o}$ to each other. They also both have one side equal in length to the smaller equilateral triangle, and these sides are also at an angle of 60$^\text{o}$ to each other.
Image

So a 60$^\text{o}$ rotation will map the blue triangle onto the red triangle. So the two triangles must be congruent. So the third sides, which are the red lengths, must be equal.
Using 'side angle side'
Let the sides of the larger equilateral triangle have length $a$ and the sides of the smaller equilateral triangle have length $b$, as labeled in the diagram. Notice that both the red triangle and the blue triangle contain an angle of 120$^\text{o}$ between sides of length $a$ and $b$.
Image

The lengths of the two sides and the size of the angle in between them uniquely define a triangle (imagine putting the ends of two sticks together at a fixed angle, joining the other ends of the sticks would complete the triangle). So the two triangles must be congruent, which means the third lengths must also be the same.
