When the boat comes in
When you pull a boat in using a rope, does the boat move more quickly, more slowly, or at the same speed as you?
Problem
Imagine you are pulling a boat in along a jetty, like in the picture below.
Image
When you move 1 metre to the right, does the boat move more than 1 metre, less than 1 metre, or exactly 1 metre?
Student Solutions
Using Pythagoras' Theorem
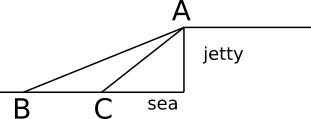
This diagram shows the 'before' and 'after' positions of the boat at B and C respectively. The boat has travelled the distance BC.
Image
In the version below, the sides of the two right-angled triangles have been labelled.
Image
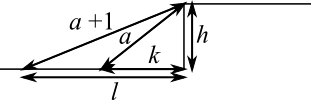
Applying Pythagoras' Theorem to the 'before' triangle, $l^2+h^2=(a+1)^2=a^2+2a+1$.
Applying Pythagoras' Theorem to the 'after' triangle, $k^2+h^2=a^2$.
Subtracting the 'after' equation from the 'before' equation, $l^2-k^2=2a+1$, so $l^2=k^2+2a+1$.
If $l=k+1$, then $l^2$ would equal $(k+1)^2=k^2+2k+1$.
In fact, $l^2=k^2+2a+1$, and since $a$ is the hypotenuse, it is longer than $k$, so $2a>2k.$ So $l^2>k^2+2k+1$, so $l>k+1$. So the boat has moved more than 1 metre.
Using a diagram (and the triangle inequality)
This diagram shows the 'before' and 'after' positions of the boat at B and C respectively. The boat has travelled the distance BC.
Image

The length AC has been rotated onto the line AC, so that the two blue line segments are the same length. The length marked on is 1 metre because the blue length (equal to AC) is 1 metre shorter than AB, because you have pulled the rope along 1 metre.
Imagine starting at B and travelling to A. It will clearly be shorter to go along the line AB than along the line BC and then along the blue line. So 1 metre must be shorter than BC. So the boat moves more than 1 metre.
Using the triangle inequality and algebra
This diagram shows the 'before' and 'after' positions of the boat at B and C respectively. The boat has travelled the distance BC.
Image

Because the rope has been pulled 1 metre along, AB = AC + 1.
ABC forms a triangle, so AB must be shorter than AC + BC.
So AC + 1 is shorter than AC + BC, which means that 1 must be shorter than BC.
So the boat moves by more than 1 metre.
