Petrol stop

Answer: 1 hour and 10 minutes

Using a distance-time graph

Image

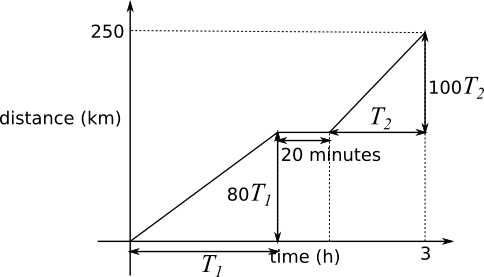
Gradient represents speed so gradients are $80$ and $100$

So vertical distances are $80T_1$ and $100T_2$

time: $T_{1}+T_{2}=3$ hours$-20$ minutes $=2\frac23$ hours

distance: $80T_{1}+100T_{2}=250\Rightarrow 8T_1+10T_2=25$

$T_1+T_2 = 2\frac23$    $\times8$ gives $8T_1+8T_2=16\tfrac{16}3=21\frac13$

Subtracting, $$\begin{align}(8T_1+10T_2) - (8T_1+8T_2)&=25 - 21\tfrac13\\

2T_2&=3\tfrac23=\tfrac{11}3\\

T_2&=\tfrac{11}6\end{align}$$ $\frac{11}6$ hours $=1$ hour and $50$ minutes.

Using a speed-time graph

Image

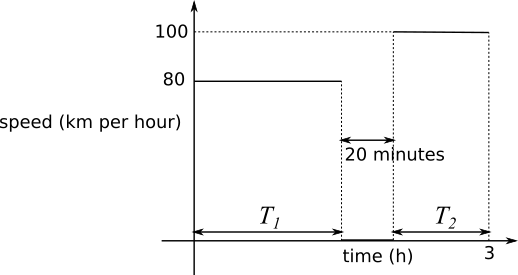
time: $T_{1}+T_{2}=3$ hours$-20$ minutes $=2\frac23$ hours

Distance on a speed-time graph is given by the area under the graph, so: $$\begin{align} 80T_{1}+100T_{2}&=250\\

\Rightarrow 80(T_1+T_2) + 20T_2&=250\\

\Rightarrow 80\times 2\tfrac23+20T_2&=250\\

\Rightarrow 8\times \tfrac83 + 2T_2 &=25\\

\Rightarrow 2T_2&= \tfrac{75}3-\tfrac{64}3\\

\Rightarrow T_2 &= \tfrac{11}6\end{align}$$ $\frac{11}6$ hours $=1$ hour and $50$ minutes.

Using the speed-distance-time relationship

Distance = speed $\times$ time

Distance travelled before the petrol stop is $80\times T_{1}$

Distance travelled after the petrol stop is $100\times T_{2}$

Total distance is $250$ km so $80T_{1}+100T_{2}=250$.

Total time is $3$ hours. $20$ minutes $=\frac13$ hour, so $T_{1}+T_{2}=2\frac23$.

$T_{1}+T_{2}=2\frac23\Rightarrow T_1 = \frac83 - T_2$

Substitute into other equation: $$\begin{align} 80 \left(\tfrac83 - T_2\right) +100T_2 &= 250\\

\Rightarrow \tfrac {64}3 -8T_2 +10T_2 &=25\\

\Rightarrow \tfrac{64}3 + 2T_2&=\tfrac{75}3\\

\Rightarrow T_2&=\tfrac{11}{6}\end{align}$$ $\frac{11}6$ hours $=1$ hour and $50$ minutes.