Folded rectangle
Can you find the perimeter of the pentagon formed when this rectangle of paper is folded?
Age
14 to 16
Challenge level
Problem
A rectangular piece of paper, 3 cm by 4 cm, is folded along its diagonal, as shown below.
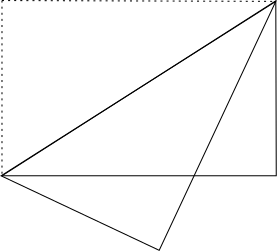
What is the perimeter of the pentagon formed (shown below in blue)?
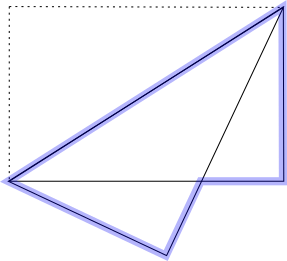
This problem is adapted from the World Mathematics Championships
Image
What is the perimeter of the pentagon formed (shown below in blue)?
Image
This problem is adapted from the World Mathematics Championships
Student Solutions
By Pythagoras' Theorem, the diagonal side on the yellow triangle below is $\sqrt{3^2+4^2}=5$ cm.
In the diagram below, the red triangles are similar. The length marked $x$ is required to find the perimeter of the pentagon.
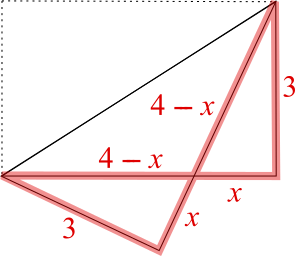
By Pythagoras' Theorem, $(4-x)^2=3^2+x^2$.
$$\begin{align}&(4-x)^2=3^2+x^2\\
&\Rightarrow16-8x+x^2=9+x^2\\
&\Rightarrow7=8x\\
&\Rightarrow x=\frac{7}{8}\end{align}$$
So the perimeter of the pentagon is $5+3+\dfrac{7}{8}+\dfrac{7}{8}+3=12\dfrac{3}{4}$ cm.
Image
In the diagram below, the red triangles are similar. The length marked $x$ is required to find the perimeter of the pentagon.
Image
By Pythagoras' Theorem, $(4-x)^2=3^2+x^2$.
$$\begin{align}&(4-x)^2=3^2+x^2\\
&\Rightarrow16-8x+x^2=9+x^2\\
&\Rightarrow7=8x\\
&\Rightarrow x=\frac{7}{8}\end{align}$$
So the perimeter of the pentagon is $5+3+\dfrac{7}{8}+\dfrac{7}{8}+3=12\dfrac{3}{4}$ cm.