Triangular Intersection
What is the largest number of intersection points that a triangle and a quadrilateral can have?
Problem
The triangle and the quadrilateral in the diagram below have 4 intersection points.
Image
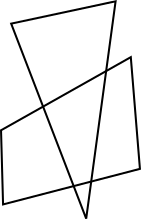
What is the largest number of intersection points that a triangle and a quadrilateral can have?
This problem is adapted from the World Mathematics Championships
Student Solutions
Every quadrilateral is made up of 4 lines, and extending these lines on beyond the vertices of the quadrilaterals is helpful to explain why there cannot be more than 8 intersection points.
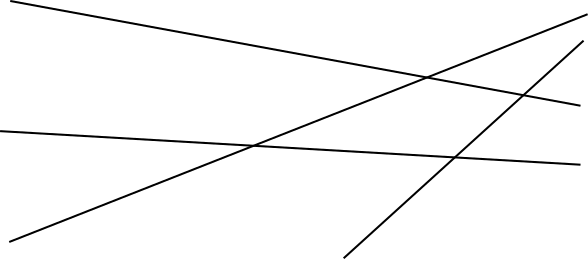
Starting from one of its vertices, a triangle can be drawn anywhere without taking the pencil off the paper, but must finish where it started.
This means that every line crossed must be crossed back again - so each of the 4 lines which make up the quadrilateral must be crossed an even number of times.
The triangle only has 3 sides, so it cannot cross any of the lines which make up the quadrilateral more than 3 times. So each of the lines which make up the quadrilateral must be crossed 0 or 2 times.
If each side is crossed 2 times, that makes a total of 8 intersection points - so there can never be more than 8 intersection points.
An example of a triangle and a quadrilateral with 8 intersection points is shown below.
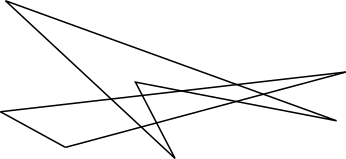
Image

Starting from one of its vertices, a triangle can be drawn anywhere without taking the pencil off the paper, but must finish where it started.
This means that every line crossed must be crossed back again - so each of the 4 lines which make up the quadrilateral must be crossed an even number of times.
The triangle only has 3 sides, so it cannot cross any of the lines which make up the quadrilateral more than 3 times. So each of the lines which make up the quadrilateral must be crossed 0 or 2 times.
If each side is crossed 2 times, that makes a total of 8 intersection points - so there can never be more than 8 intersection points.
An example of a triangle and a quadrilateral with 8 intersection points is shown below.
Image

