Backwards laps
If two friends run in opposite directions around a track, and they pass each other every 24 seconds, how long do they take to complete a lap?
Problem
Chris and Sophie are running in opposite directions around a track, with constant speeds. Chris notices that he passes Sophie every 24 seconds.
It takes Chris 60 seconds to complete each lap.
How long does it take Sophie to complete each lap?
Student Solutions
Answer: 40 seconds
Using proportion
In 24 seconds:
Image

Chris runs $\frac{24}{60}=\frac{2}{5}$ of a lap in 24 seconds
Sophie runs $1-\frac25=\frac{3}{5}$ of a lap in 24 seconds
$\frac{1}{5}$ of a lap in 24$\div$3 = 8 seconds
1 whole lap in 8$\times$5 = 40 seconds
OR
Chris runs $\frac25$ of a lap while Sophie runs $\frac35$ of a lap
$\therefore$ the distances they run in a fixed time are in the ratio $2:3$
$\therefore$ the times they take to run a fixed distance are in the ratio $3:2$
$3:2$ is equivalent to $60:40$
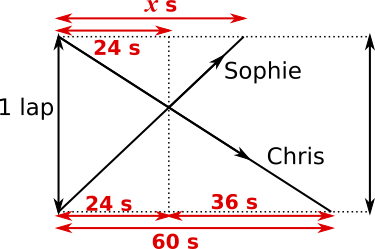
Using a Travel Diagram
The diagram below shows time horizontally and distance vertically, with lines sloping in opposite directions for Sophie's journey and Chris' journey, because they run in opposite directions.
They begin one full lap apart, which is actually when they are in the same place, and their paths cross again after 24 seconds.
The triangles coloured yellow in the diagram below are congruent, because of the symmetry in the diagram.
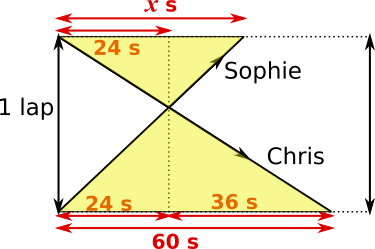
So, using scale factors within the triangles, $\dfrac{x}{24}=\dfrac{60}{36}\Rightarrow x=\dfrac{60}{36}\times24=40$
Or using scale factors between the triangles, $\dfrac{x}{60}=\dfrac{24}{36}\Rightarrow x=\dfrac{24}{36}\times60 = 40$
So Sophie runs a lap in 40 seconds.
Sophie runs $1-\frac25=\frac{3}{5}$ of a lap in 24 seconds
$\frac{1}{5}$ of a lap in 24$\div$3 = 8 seconds
1 whole lap in 8$\times$5 = 40 seconds
OR
Chris runs $\frac25$ of a lap while Sophie runs $\frac35$ of a lap
$\therefore$ the distances they run in a fixed time are in the ratio $2:3$
$\therefore$ the times they take to run a fixed distance are in the ratio $3:2$
$3:2$ is equivalent to $60:40$
Using a Travel Diagram
The diagram below shows time horizontally and distance vertically, with lines sloping in opposite directions for Sophie's journey and Chris' journey, because they run in opposite directions.
They begin one full lap apart, which is actually when they are in the same place, and their paths cross again after 24 seconds.
Image

The triangles coloured yellow in the diagram below are congruent, because of the symmetry in the diagram.
Image

So, using scale factors within the triangles, $\dfrac{x}{24}=\dfrac{60}{36}\Rightarrow x=\dfrac{60}{36}\times24=40$
Or using scale factors between the triangles, $\dfrac{x}{60}=\dfrac{24}{36}\Rightarrow x=\dfrac{24}{36}\times60 = 40$
So Sophie runs a lap in 40 seconds.
