Laps
On which of the hare's laps will she first pass the tortoise?
Problem
The hare and the tortoise start running together around a 300m track.
The hare runs at a constant speed of 15 km/h and the tortoise runs at a constant speed of 13.8 km/h.
On which of the hare's laps will she first pass the tortoise?
This problem is adapted from the World Mathematics Championships
Student Solutions
Answer: On the hare's 13th lap
How far the tortoise goes for each hare lap using speed distance time
Hare 15 km in 1 hour
1 km in 4 minutes
250 m in 1 minute
300 m in 1$\frac15$ minutes
Tortoise 13.8 km in 1 hour
13800 m in 1 hour
13800$\div$60 m in 1 minute
230 m in 1 minute
230 + $\frac{230}5$ = 276 m in 1$\frac15$ minutes
The tortoise loses 24 m every time the hare runs a lap
Image
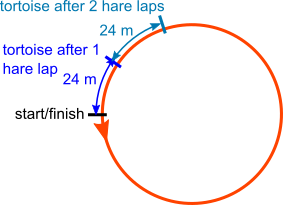
24 $\times$ 12 = 288 $\lt$ 300
24 $\times$ 13 $\gt$ 300
Image

So the tortoise does not reach the starting point on the hare's 13th lap
So the hare passes the tortoise on the hare's 13th lap.
How far the tortoise goes for each hare lap using inverse proportion
hare speed : tortoise speed is $15 : 13.8$
hare distance : tortoise distance is $13.8:15$, which is equivalent to $23:25$
So every time the hare runs a lap, the tortoise runs $\frac{23}{35}$ of a lap
Image
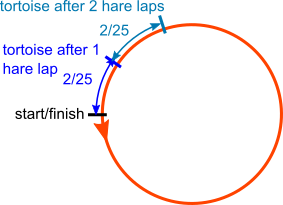
$\frac2 {25}\times12 \lt 1$
$\frac2{25}\times13\gt1$
Image
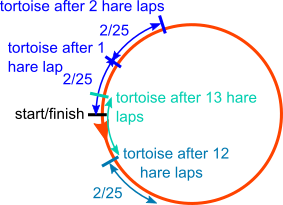
So the tortoise does not reach the starting point on the hare's 13th lap
So the hare passes the tortoise on the hare's 13th lap.
After how long has the hare travelled 300 m further than the tortoise?
$t$ time (in hours)
hare distance $=15t$
tortoise distance $=13.8t$
hare first passes tortoise when hare is $300$ metres = $0.3$ km ahead $$\begin{align} &15t-13.8t=0.3\\
\Rightarrow &1.2t = 0.3\\
\Rightarrow & t= \tfrac{0.3}{1.2}=\tfrac14\end{align}$$ When $t=\frac14$ the hare has run $15\times\frac14 = 3\frac34$ km or $3750$ metres
$3600$ m $= 12$ laps
$3900$ m $=13$ laps
So the hare was on her thirteenth lap.
Working out how long it takes each runner to run $k$ laps
Hare runs 15km in 1 hour
15000 m in 1 hour
300 m in $\frac{1}{50}$ hours.
Tortoise runs 13.8 km in 1 hour
13800 m in 1 hour
300 m in $\frac{1}{46}$ hours.
Hare runs $k$ laps in $\frac{1}{50}\times k$ hours.
When the hare passes the tortoise, the tortoise has only run $k-1$ laps.
Tortoise runs $k-1$ laps in $\frac{1}{46}\times(k-1)$ hours. $$\begin{align}&\tfrac{1}{50}k=\tfrac{1}{46}(k-1)\\
\Rightarrow&46k=50(k-1)\\
\Rightarrow&46k=50k-50\\
\Rightarrow &40=4k\\
\Rightarrow &12.5=k\end{align}$$So the hare has run $12.5$ laps and is on her thirteenth when she passes the tortoise.
