Boys and Girls

Answer: 1300

Using letters to represent the 'parts'

Image

 

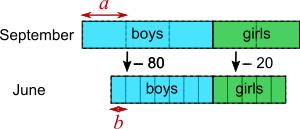
Boys: $3a-80=7b$            $\times2$ gives $6a-160=14b$

Girls: $2a - 20 = 5b$            $\times3$ gives $6a-60=15b$

Subtract: $(6a-60)-(6a-160)=15b-14b$

                                           $100=b$

In June there were $7b + 5b = 12b = 1200$ students

In September there were $1200 + 20 + 80 = 1300$ students

Using a letter to represent the number of students in September

Image

  

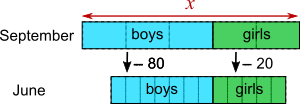
September: $\frac35x$ boys out of $x$ students

June: $\frac35x-80$ boys is $\frac7{12}$ of $x-100$ students

$$\begin{align}\dfrac{\tfrac35x-80}{x-100}&=\dfrac7{12}\\

\Rightarrow 12\times\left(\tfrac35x-80\right)&=7\times\left(x-100\right)\\

\Rightarrow 12\times\left(3x-4000\right)&=35\times\left(x-100\right)\\

\Rightarrow 36x-4800&=35x-3500\\

\Rightarrow x&=1300\end{align}$$

Using letters to represent the numbers of boys and girls in September

Image

 

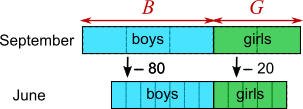
September: $B:G$ is $3:2$, and so $\frac B3=\frac G2\Rightarrow B=\frac{3G}2$

June: $B-80:G-20$ is $7:5$, so $\frac{B-80}7=\frac{G-20}5$

                                            $\Rightarrow 5(B-80)=7(G-20)$

                                            $\Rightarrow 5B-260=7G$

Substitute $B=\frac{3G}2$: $$\begin{align}5\tfrac{3G}2-260&=7G\\

\Rightarrow 15G-520&=14G\\

\Rightarrow G &= 520\end{align}$$

So $B=\frac{3G}2=780$ and in September there were $520 + 780 =1300$ students.