3-4-5 circle
Can you find the radius of the circle inscribed inside a '3-4-5 triangle'?
Problem
A circle is drawn inside a right-angled triangle so that each side of the triangle is a tangent to the circle, as shown in the diagram.
The sides of the triangle are 3, 4 and 5 units long, as shown.
Find the radius of the circle.
Image
This problem is adapted from the World Mathematics Championships
Student Solutions
Using area
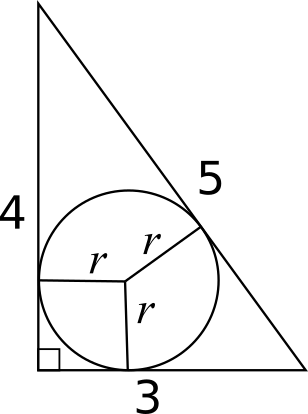
Imagine drawing lines from each vertex to the centre of the circle, as shown below.

This gives us 3 triangles all of height $r$ and of bases $3, 4$ and $5$ respectively (the angle between the radius and the tangent is $90^\text{o}$, so these can be considered the bases and heights). Thus, the areas of the triangles are $\frac{1}{2}\times 3r$, $\frac{1}{2}\times 4r$ and $\frac{1}{2}\times 5r$ respectively.
The whole triangle has area $\frac{1}{2} \times 3 \times 4 = 6$.
We know that the areas of the smaller triangles must sum to give the area of the whole triangle so we have that:
$\frac{1}{2}\times 3r + \frac{1}{2}\times 4r + \frac{1}{2}\times 5r = 6$
$\Rightarrow \frac{1}{2}\times 12r = 6$
$\Rightarrow 6r=6$
$\Rightarrow r=1$.
Using perimeter
The angle between a radius and a tangent is $90^\circ$, which is shown on the diagram below.
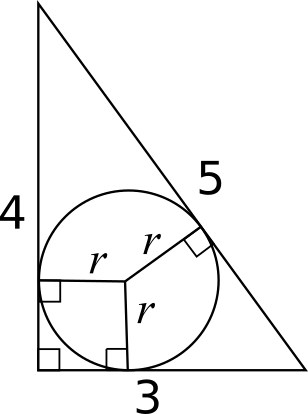
Three of the angles in the quadrilateral at the bottom left are right angles, so the fourth angle must be a right angle too. This means that it must be a square, since two adjacent sides both have length $r$.
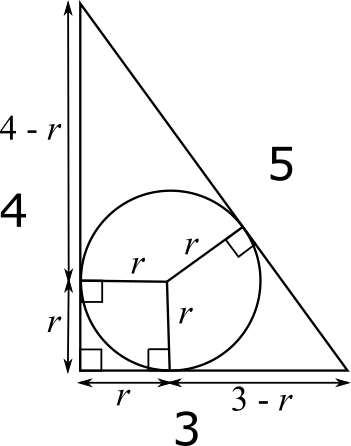
This is shown in the diagram below, and the other parts of the sides of length 3 and 4 are also shown in terms of $r$.
Using symmetry, or the circle theorem that the lengths of two tangents drawn from a point to the circumference are equal, or by drawing a line from the vertex to the centre and observing similar triangles, these lengths can also be labelled on the side of length 5, as shown below.
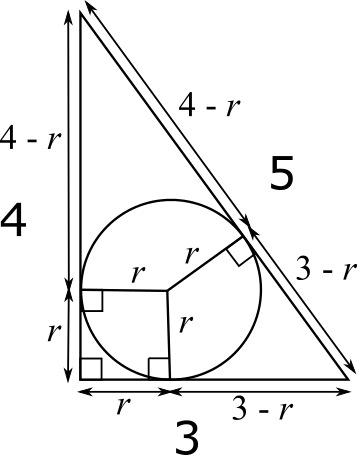
This means that $4-r$ and $3-r$ must add up to 5, so
$4-r+3-r=5$, so $7-2r=5$, so $2r=2$, so $r=1$.
Imagine drawing lines from each vertex to the centre of the circle, as shown below.
Image

This gives us 3 triangles all of height $r$ and of bases $3, 4$ and $5$ respectively (the angle between the radius and the tangent is $90^\text{o}$, so these can be considered the bases and heights). Thus, the areas of the triangles are $\frac{1}{2}\times 3r$, $\frac{1}{2}\times 4r$ and $\frac{1}{2}\times 5r$ respectively.
The whole triangle has area $\frac{1}{2} \times 3 \times 4 = 6$.
We know that the areas of the smaller triangles must sum to give the area of the whole triangle so we have that:
$\frac{1}{2}\times 3r + \frac{1}{2}\times 4r + \frac{1}{2}\times 5r = 6$
$\Rightarrow \frac{1}{2}\times 12r = 6$
$\Rightarrow 6r=6$
$\Rightarrow r=1$.
Using perimeter
The angle between a radius and a tangent is $90^\circ$, which is shown on the diagram below.
Image

Three of the angles in the quadrilateral at the bottom left are right angles, so the fourth angle must be a right angle too. This means that it must be a square, since two adjacent sides both have length $r$.
This is shown in the diagram below, and the other parts of the sides of length 3 and 4 are also shown in terms of $r$.
Image

Using symmetry, or the circle theorem that the lengths of two tangents drawn from a point to the circumference are equal, or by drawing a line from the vertex to the centre and observing similar triangles, these lengths can also be labelled on the side of length 5, as shown below.
Image

This means that $4-r$ and $3-r$ must add up to 5, so
$4-r+3-r=5$, so $7-2r=5$, so $2r=2$, so $r=1$.
