Coloured Black
An ink stamp draws out a shape when it is rotated. What is its area?
Age
14 to 16
Challenge level
Problem
A square ink stamp has sides of length 1 cm.
It is covered in black ink and carefully placed in the middle of a piece of white paper.
The stamp is then rotated $180^o$ about one of its corners so that all of the square remains in contact with the paper throughout the turn, leaving a black trail.
The stamp is then removed from the paper.
What area of paper, in cm$^2$, is coloured black?
This problem is taken from the UKMT Mathematical Challenges.
Student Solutions
Image
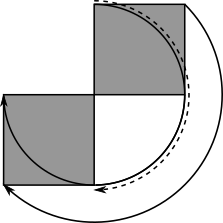
This diagram shows the paths of the three corners that are not the centre of rotation as the ink stamp is rotated.
Image
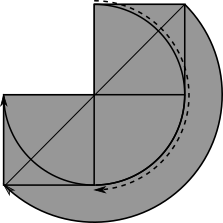
Everything within the large semicircle, or the beginning and ending positions of the stamp will be coloured black.
The radius of the semicircle is equal to the diagonal of the ink stamp.
Since the sides of the stamp are all $1$ cm, we can find the length of the diagonal using Pythagoras' Theorem: $1^2+1^2=r^2\Rightarrow 2=r^2\Rightarrow r=\sqrt{2}$ cm
The area of the semicircle is half of the area of a full circle of radius $\sqrt{2},$ so half of $\pi\sqrt{2}^2,$ which is half of $2\pi,$ which is $\pi$ cm$^2.$
The total area is the area of the semicircle plus the areas of the two half-squares that stick out above it. Each square has area $1$ cm$^2,$ so the two halves together have area $1$ cm$^2.$
So the total area is $(\pi+1)$ cm$^2.$