Question of Three Sides
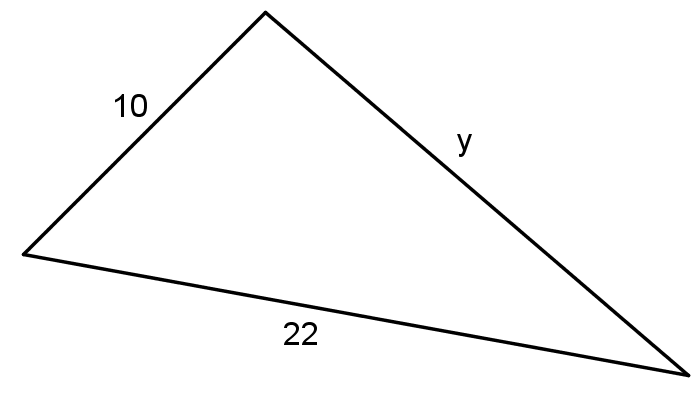
Can you find the length of the third side of this triangle?
Problem
The triangle shown has an area of 88 square units.
Image
Student Solutions
Using Pythagoras' Theorem on two parts of the triangle
The area of a triangle is $\frac{1}{2}$base$\times$height, so taking the base of the triangle as the side of length $22,$ drawing on the height splits the triangle into two right-angled triangles:
Image
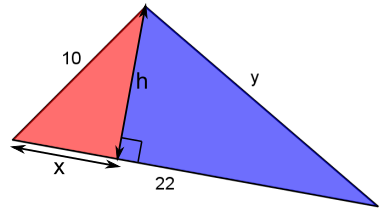
$\frac{1}{2}\times22\times h=88$
$\Rightarrow 11\times h=88$
$\Rightarrow h=8$
The base of the red triangle can be found using Pythagoras' theorem, and then we will know the base of the blue triangle (since they add up to $22$), so we can use Pythagoras' Theorem again to find $y.$
$x^2+8^2=10^2$
$\Rightarrow x^2 =10^2-8^2 = 36$
so $x=6$
So the base of the blue triangle must be $16.$
So $8^2+16^2=y^2$
$\Rightarrow 320=y^2$
$\Rightarrow y=\sqrt{320},$
which is equal to $8\sqrt{5}$ or $17.89$ (2 d.p.).
Using trigonometry
In the diagram below, the triangle has been labelled to make substitution into the trigonometric formulae easier.
Image
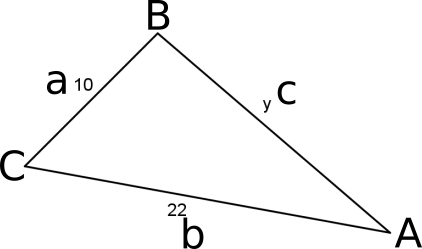
Using the formula for the area of a triangle $\frac{1}{2}ab\sin{C}$, $\frac{1}{2}\times10\times22\times\sin{C}=88\Rightarrow 110\sin{C}=88\Rightarrow\sin{C}=0.8,$ so $C=53.13^\text{o}.$
Then using the cosine rule $c^2=a^2+b^2-2ab\cos{C},$ $$\begin{align}&y^2=10^2+22^2-2\times10\times22\times\cos{53.13^\text{o}}\\
\Rightarrow&y^2=100+484-440\times0.6\\
\Rightarrow&y^2=320\\
\Rightarrow&y=\sqrt{320}=8\sqrt{5}\approx17.89\end{align}$$
