Stacking Shapes
Weekly Problem 28 - 2017
The diagram on the right shows an equilateral triangle, a square and a regular pentagon. What is the sum of the interior angles of the resulting polygon?
The diagram on the right shows an equilateral triangle, a square and a regular pentagon. What is the sum of the interior angles of the resulting polygon?
Age
11 to 14
Challenge level
Problem
Image
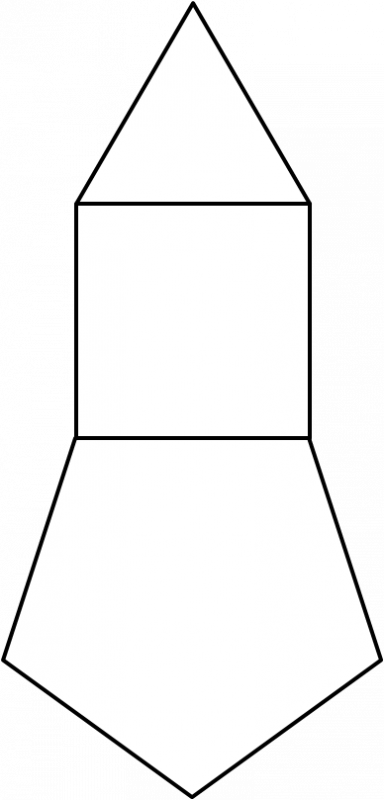
What is the sum of the interior angles of the resulting polygon?
If you liked this problem, here is an NRICH task that challenges you to use similar mathematical ideas.
Student Solutions
Image
The three blue angles are the interior angles of a triangle, so add up to $180^\circ$.
The four red angles are the interior angles of a square, which is a type of quadrilateral, so add up to $360^\circ$.
The five green angles are the interior angles of a pentagon, so add up to $540^\circ$.
Therefore, the total interior angle is $180^\circ + 360^\circ + 540^\circ = 1080^\circ$.
Since the shapes are regular, the angles could be individually counted. The blue angles are all $60^\circ$, the red angles are all $90^\circ$ and the green angles are all $108^\circ$.