Parallel Base
Weekly Problem 46 - 2015
The diagram shows two parallel lines and two angles. What is the value of x?
The diagram shows two parallel lines and two angles. What is the value of x?
Problem
In the diagram $ST$ is parallel to $UV$.
Image
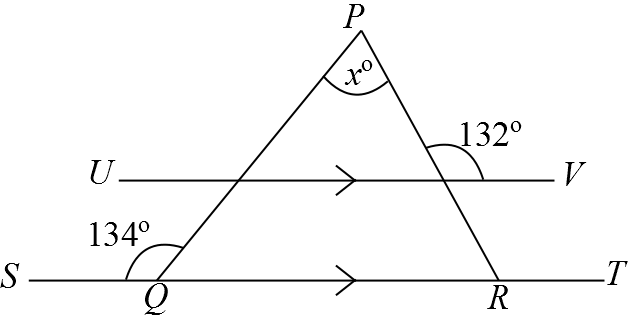
What is the value of $x$?
If you liked this problem, here is an NRICH task that challenges you to use similar mathematical ideas.
Student Solutions
Since $ST$ is parallel to $UV$, $\angle PRT$ and the angle of size $132^{\circ}$ are corresponding angles, so $\angle PRT=132^{\circ}$.
Since angles on a straight line sum to $180^{\circ}$ we must have $\angle PRQ=48^{\circ}$.
From the exterior angle of a triangle theorem, $\angle SQP=\angle QPR + \angle PRQ$,
so $134=x+48$, that is, $x=86$.
