Radioactive triangle
Weekly Problem 41 - 2014
Three straight lines divide an equilateral triangle into seven regions. What is the side length of the original triangle?
Three straight lines divide an equilateral triangle into seven regions. What is the side length of the original triangle?
Age
11 to 14
Challenge level
Problem
Image
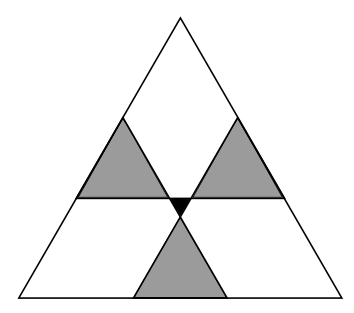
The diagram shows a large equilateral triangle divided by three straight lines into seven regions. The three grey regions are equilateral triangles with sides of length $5\;\mathrm{cm}$ and the central black region is an equilateral triangle with sides of length $2\;\mathrm{cm}$.
What is the side length of the original large triangle?
If you liked this problem, here is an NRICH task that challenges you to use similar mathematical ideas.
Student Solutions
Image
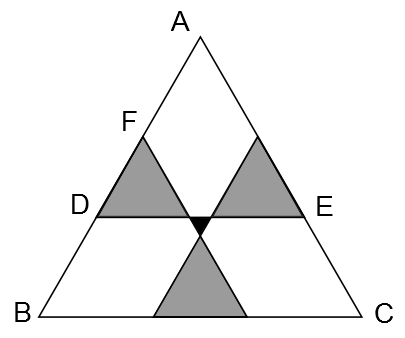
As triangle ABC is equilateral, ∠BAC = $60$ °. Since the grey triangles are equilateral, ∠ADE = $60$ °, so the triangle ADE is equilateral.
The length of the side of this triangle is equal to the length of $DE = (5 + 2 + 5)\;\mathrm{cm} = 12\;\mathrm{cm}$. So $AF = AD - FD = (12 - 5)\;\mathrm{cm} = 7\;\mathrm{cm}$.
By a similar argument, we deduce that $BD = 7\;\mathrm{cm}$, so the length of the side of the triangle $ABC = (7 + 5 + 7)\;\mathrm{cm} = 19\;\mathrm{cm}$.