Isosceles reduction
Weekly Problem 29 - 2010
An isosceles triangle is drawn inside another triangle. Can you work out the length of its base?
An isosceles triangle is drawn inside another triangle. Can you work out the length of its base?
Age
14 to 16
Challenge level
Problem
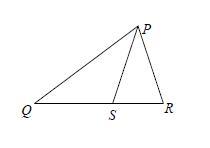
$PQR$ is a triangle and $S$ is a point on $QR$.
$QP=QR=9$ cm and $PR = PS =6$ cm.
What is the length of $SR$?
Image
If you liked this problem, here is an NRICH task which challenges you to use similar mathematical ideas.
Student Solutions
Triangles $PRS$ and $QPR$ are similar because $\angle PSR = \angle QRP$ (since $PR =PS$) and $\angle PRS = \angle QPR$ (since $QP =QR$).
Hence $\frac{SR}{RP} = \frac{RP}{PQ}$, that is $\frac{SR}{6} = \frac{6}{9}$, that is $SR = 4$.