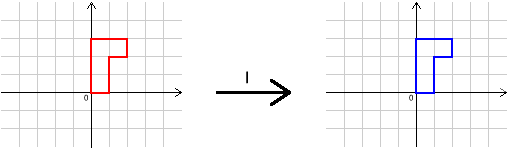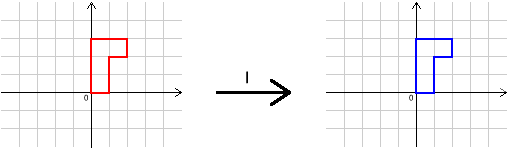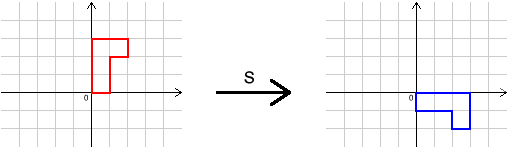We wrote the October 2006 Stage 3 problems (Decoding Transformations , Combining Transformations and Simplifying Transformations ) with some more advanced (and more general) mathematics in mind; here, we shall try to introduce that maths and explain how it relates to the problems. If you haven't already tried the problems, I suggest that you look at them now.

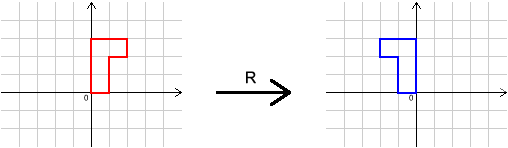
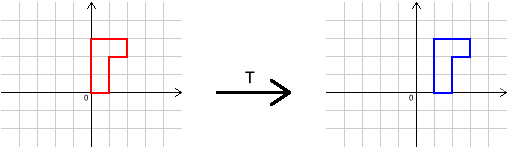
In the problems, you were introduced to four transformations: $I$, $R$, $S$ and $T$. Here is a reminder of what they are.

Transformation R - reflection in the y-axis

Transformation S - rotation by 90 degrees clockwise about the origin

Transformation T - translation by one unit to the right

In the course of tackling the three problems, we hope that you will have discovered some important properties of the transformations made up from $I$, $R$, $S$ and $T$. Here is a summary.

\begin{itemize} \item[(i)] Doing two or more of these transformations one after another gives another transformation. \item[(ii)] If $A$, $B$ and $C$ are transformations then $(A B)C=A(B C)$. That is, doing transformations one after another is associative. \item[(iii)] If $A$ is a transformation, then $A I=A=I A$. That is, $I$ is the \emph{identity transformation}. \item[(iv)] Each transformation $A$ has a transformation $B$ that undoes it, that is, with $A B=I=B A$. We say that $B$ is the \emph{inverse} of $A$. \end{itemize}

We didn't really draw attention to properties (i) and (ii) in the problems, as they are quite clear in this context - in fact, it is probably harder to realise that they might not always be true than it is to realise that they are true here!

Why are we interested in these properties? Well, there are lots more contexts in which these properties hold. If we can prove a theorem just assuming these properties, then we'll be able to apply it to any situation with these properties. It turns out that this is an extremely powerful idea - indeed, it underlies much of the mathematics studied at university.

So let's try to make a formal definition of these properties.

We shall define a group . A group is a set $G$ together with a binary operation $\bullet$ that satisfies three$^{(1)}$ axioms.

We've just used lots of scary words, so let's pause for a moment to understand them.

A set is just a collection of objects. For example, it could be the set of all whole numbers, or the set of all fractions, or, as above, a set of transformations.

A binary operation is a rule for combining two members of the set to give another member of the set.

Here are some examples of sets with binary operations.

\begin{itemize} \item[(a)] $G=$ set of all whole numbers, $\bullet=$ addition, or $\bullet=$ multiplication. \item[(b)] $G=$ set of all fractions, $\bullet=$ addition, or $\bullet=$ multiplication. \item[(c)] $G=$ set of all whole numbers, $\bullet$ is defined by $a\bullet b=a^b$. \item[(d)] $G=$ set of all positive whole numbers, $\bullet=$ addition. \item[(e)] $G=$ set of all transformations obtained by repeatedly doing $R$, $S$, $T$ and their inverses (including $I$, of course), $\bullet=$ composition (so $R\bullet S=R$ followed by $S$ etc.). \end{itemize}

Note that if $G$ is the set of all whole numbers then division is not a binary operation: whilst it takes two members of the set and combines them, it doesn't always return a member of the set. (For example, 1 divided by 2 is $\frac{1}{2}$ - not a whole number!)

Now let's list the axioms. Here, ``axiom'' just means ``condition''. Remember that these are the conditions that a set and binary operation have to satisfy in order to form a group.

\begin{itemize} \item[Axiom 1:] $\bullet$ is associative. That is, $(a\bullet b)\bullet c=a\bullet (b\bullet c)$ for all $a$, $b$ and $c$ in $G$. \item[Axiom 2:] There is some $e$ in $G$ such that $e\bullet a=a =a\bullet e$ for all $a$ in $G$. (We call $e$ an identity for $\bullet$.) \item[Axiom 3:] For each $a$ in $G$, there is a $b$ in $G$ such that $a\bullet b=e=b\bullet a$. (We call $b$ an \emph{inverse} for $a$.) \end{itemize}

Let's go back to our examples to decide which of them are groups (that is, which of them satisfy these conditions). You might like to try this for yourself before reading on.

\begin{itemize} \item[(a)] $G=$ set of all whole numbers, $\bullet=$ addition.

We have $a+(b+c)=(a+b)+c$ for all whole numbers $a$, $b$ and $c$.

We have an identity, 0: $0+a=a=a+0$ for all whole numbers $a$.

For each whole number $a$, we have an inverse, $-a$: $a+ -a=0=-a+a$.

So this is a group.

What about $\bullet=$ multiplication?

It's associative, and 1 is an identity here, but we don't always have inverses.

For example, there is no whole number $b$ such that $2b=1$. So this is not a group - the operation really does make a difference.

\item[(b)] These are both groups; try to show this yourself.

\item[(c)] This is not a group: $\bullet$ here is not associative. (It fails the other conditions too.)

For example, $2\bullet(3\bullet 4) =2\bullet 3^4=2\bullet 81=2^{81}$, but $(2\bullet 3)\bullet 4=2^3\bullet 4=(2^3)^4=2^{12}\neq 2^{81}$.

\item[(d)] This is not a group: there's no identity.

\item[(e)] This is a group - we talked about it earlier! \end{itemize}

By the way, notice that we didn't require $\bullet$ to have the property that $a\bullet b=b\bullet a$. (That is, we didn't require $\bullet$ to be commutative.) In fact, the transformations in our original example didn't have this property. If $\bullet$ is commutative, then we say that the group is abelian (named after the Norwegian mathematician Niels Abel).

Groups don't have to be infinite. If you've come across modulo arithmetic (or clock arithmetic), then you can show that the numbers 0, 1, 2, 3 and 4 form a group under addition mod 5.

Going back to our transformations, the group of transformations made up just from $R$ and $S$ (including $I$) is a finite group - if you've solved the problem Simplifying Transformations then you'll have seen that it has just 8 elements. We say that it has order 8.

We're going to spend the rest of this article thinking about a result that we can prove for all finite groups - but first we're going to think about it in the context of our group of transformations made up from $R$ and $S$.

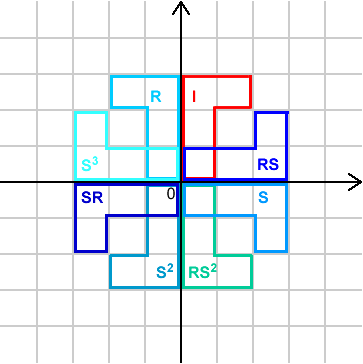
If you've done the problem Combining Transformations then hopefully you've discovered that $R^2=I$ and $S^4=I$. That is, if you do $R$ or $S$ enough times then you get the identity ($I$). Is this true of the other elements in the group? Remember that combinations like $R S S R S R S R S S S R S R S S R S S S$ can be simplified, so we can write the elements of the group as $I$, $R S$, $S$, $R S^2$, $S^2$, $S R$, $S^3$ and $R$. (Of course, there are other ways to write them, in some cases just as simply.) Their effects on the upside-down 'L' shape can be illustrated like this:

We'd like to show that if

A

is a transformation made from combining

R

and

S

then there is a positive whole number

k

such that

A^{k} = I

. (That is, if we do

A

enough times then we get the identity.) We know that we just need to check the cases when

A

is one of the eight transformations listed (and pictured) above.

$A = I$ is easy, and we've already done $A = R$ and $A = S$ ( $R^{2} = I$ and $S^{4} = I$ ).

From the diagram, we see that $A = R S$ is a reflection in the line $y = x$ , and so $A^{2} = I$ . (Algebraically, we have $A^{2} = (R S) (R S) = (S^{3} R) (R S) = S^{3} (R^{2}) S = S^{4} = I$ , using the relation $R S = S^{3} R$ introduced in Simplifying Transformations.)

$A = R S^{2}$ is a reflection in the $x$ -axis, so $A^{2} = I$ (algebraically, $A^{2} = (R S^{2}) (R S^{2}) = (S^{3} R S) (S^{3} R S) = S^{3} R (S S^{3}) R S = S^{3} (R R) S = S^{4} = I$ ).

Also, $A = S^{2}$ is a rotation by $180^{\circ}$ about the origin, so $A^{2} = S^{4} = I$ .

If $A = S R$ then $A$ is a reflection in the line $y = - x$ , so $A^{2} = (S R) (S R) = S (R S) R = S (S^{3} R) R = (S S^{3}) (R R) = I$ .

Finally, if $A = S^{3}$ then $A$ is a rotation by $90^{\circ}$ anticlockwise about the origin, so $A^{4} = (S^{3})^{4} = (S^{4})^{3} = I$ .

We have shown that if $A$ is a transformation made from combining $R$ and $S$ then there is some positive integer $k$ such that $A^{k} = I$ .

Notice that this is certainly not true for $T$ . We can do $T$ as many times as we like and we'll never get back to the identity. So there's an important property of $R$ and $S$ that makes this true.

In fact, we can prove the result for any finite group, and this is precisely what we shall do next. We'll keep referring back to our favourite group of transformations (those made from $R$ and $S$ ). For convenience, let's call this group $H$ .

Theorem
Let $G$ be a finite group (where the binary operation is $•$ ) with identity element $e$ .
Let $g$ be an element of $G$ . Write $g^{k}$ for $\underset{k times}{\underset{︸}{g • g • \dots • g}}$ .
Then there is some positive whole number $k$ such that $g^{k} = e$ . That is, if we do $g$ enough times then we get back to the identity.

(Hopefully you can see how this generalises what we have shown about transformations. Of course, in the case of transformations, $e = I$ )

Proof
Suppose that $G$ has $n$ elements.

(We know that $H$ (the group of transformations made up from $R$ and $S$ ) has 8 elements.)

We can think about $e$ , $g$ , $g^{2}$ , ..., and $g^{n}$ . There are $n + 1$ things in this list, and they are all in $G$ . So two of them must be the same, say $g^{r}$ and $g^{s}$ . That is, $g^{r} = g^{s}$ , where $r \neq s$ . We may as well assume that $r > s$ (if not, switch the labels).

(In the case of $H$ , we could think about $I$ , $S$ , $S^{2}$ , $S^{3}$ , $S^{4}$ , $S^{5}$ , $S^{6}$ , $S^{7}$ and $S^{8}$ , for example. There are 9 things here, and $H$ only has 8 elements, so two of them must be the same. For example, we know that $S^{6} = S^{2}$ . (Of course, we know some other pairs are equal too.) So in this example we have $r = 6$ and $s = 2$ .)

We can apply $g^{- 1}$ (the inverse of $g$ ) to both sides, to get $g^{r} • g^{- 1} = g^{s} • g^{- 1}$ , that is, $g^{r - 1} = g^{s - 1}$ . In fact, we can apply $g^{- 1}$ to both sides $s$ times, to get $g^{r - s} = g^{s - s} = g^{0} = e$ . (Since $g^{1} g^{- 1} = e$ , we may refer to $e$ as $g^{0}$ .)

Now $r - s$ is a positive whole number with $g^{r - s} = e$ , so there is indeed a positive whole number $k$ with $g^{k} = e$ , namely $k = r - s$ . Notice that we have shown this for any finite group, and any element within that group - that seems pretty remarkable to me!

(In our example, we can apply $S^{- 1}$ to both sides of $S^{6} = S^{2}$ , to get $S^{5} = S$ . Applying $S^{- 1}$ twice, we get $S^{4} = S^{0}$ , and we know that $S^{0} = I$ (that's what $S^{0}$ means). So $S^{4} = I$ . Of course, this isn't a surprise, but we could have used any element of $H$ (rather than $S$ ) and this argument would have worked. In the general case, we aren't able to identify which powers of $g$ are equal, we just know that some two are, which is why we have to use algebra.)

There are lots more things that can be shown about groups. In fact, there's a whole branch of maths about it - called Group Theory! People who study maths at university usually do some group theory in their first year. There are some other articles on NRICH about group theory. One is Small Groups, and another is An Introduction to Mathematical Structure.

$^{(1)}$ Note to those who have studied groups before: some people require four axioms. Observant people will notice that we have included the fourth in our definition of a binary operation.