"Can all equilateral triangles of any area be drawn on an isometric grid with vertices on the lattice points?" Don't take any solution as the last word. Like most problems, there are many ways to solve this one.

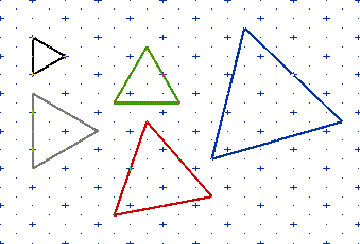
Rachel Walker, The Mount School York, found that the triangles in the diagram, have areas 1, 3, 4, 7 and 13 square units. Rachel also found that it is impossible to draw a triangle of area 2 square units with vertices on the grid points and triangles can be drawn with areas:

1, 3, 4, 7, 9, 12, 13, 16, 19, 21, 25, 27, 28, 31, 36, 37, 39, 43, 48, 49, …

The pattern in this sequence of numbers is not obvious.

From the diagram we can show that lines joining two grid points can only have certain lengths and hence equilateral triangles with vertices on the grid points can have some areas and not others.

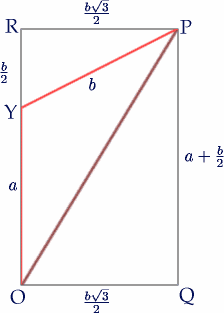
Taking any two grid points, say O and P, then we can get from O to P by a whole number of steps from O upwards to Y and then a whole number of steps from Y to P where YP is at 60 degrees to OY. From the triangles in the diagram and using Pythagoras theorem, with OY=a and YP=b, we get OP ² = a ² + b ² + ab.

We give all the areas in terms of the unit equilateral triangle which has side length one unit and area (Ö 3)/4 square units. Multiplying the side length by a factor k multiplies the area by a factor k ² so an equilateral triangle with side length Ö (a ² + b ² + ab) has area (a ² + b ² + ab) unit triangles. This is the formula for the sequence of areas given by Rachel and the table below, which can be extended indefinitely, shows areas calculated from the formula for values of a and b up to 10.

						a
		0	1	2	3	4	5	6	7	8	9	10
	0	0	1	4	9	16	25	36	49	64	81	100
	1		3	7	13	21	31	43	57	73	91	111
	2			12	19	28	39	52	67	84	103	124
	3				27	37	49	63	79	97	117	139
b	4					48	61	76	93	112	133	156
	5						75	91	109	129	151	175
	6							108	127	148	171	196
	7								147	169	193	219
	8									192	217	244
	9										243	271
	10											300

Nicola Spitlal, Madras College, investigated the areas in a different way and arrived at a version of Pick's theorem for the isometric grid. Georg Pick published his theorem in 1899 with the title "A geometrical contribution to number theory" and it beautifully brings together apparently distinct mathematical topics. For any polygon with vertices on the grid points of a square lattice, the theorem gives a formula for the area of the polygon in terms of the number of grid points on the boundary and the number of grid points inside the polygon. There is a corresponding version, which Nicola discovered, for the isometric grid and there are many different proofs of these results in the literature. Congratulations Nicola on your excellent work which is given below.

"The first thing we did was draw equilateral triangles on isometric paper. We then checked to see if there was a connection between the number of dots inside the triangle (I), the number of dots on the perimeter (P) and the area (A), measuring in 'unit triangles'.

These tables were made to record the results.

I	P	A	I	P	A	I	P	A
1	3	3	2	3	5	3	3	7
1	4	4	2	6	8	3	8	12
1	5	5	2	7	9	3	11	15
			2	8	10	3	12	16
			2	10	12
If the number of dots on the inside is one then the area is equal to the number of perimeter dots.			If the number of dots on the inside is two then the area is equal to the number of perimeter dots plus two.			If the number of dots on the inside is three then the area is equal to the number of perimeter dots plus four.

Summary of these tables
I	A
1	P+0
2	P+2
3	P+4
I	P + 2I - 2

From these cases it seems that we can find the area of an equilateral triangle using the formula A = P + 2I - 2 (area equals the number of dots on the perimeter plus twice the number of dots inside the triangle, minus 2)."

Nicola then systematically drew triangles on an isometric grid so as gradually to increase their size, to check this formula and to show which areas are possible and which are not.