Well done to Trevor from Riccarton High
School, and also to Erin, for dealing with each of the three
coordinates one at a time.
Keeping two coordinates fixed, while
changing the third coordinate and noticing whether the distance
to the target metagiff increased or decreased, then stopping when
no further decrease is possible, certainly locates the target in
the end.
Once we have a method that works the next
challenge is to locates the target using the minimum number of
guesses.
Michael used algebra to do this.
I needed to draw a diagram to follow his
algebra, here is the diagram I drew.
(Remember wherever possible to include a
diagram to help readers follow your working)
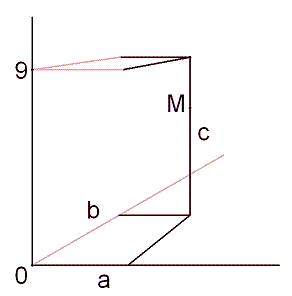
If the metagiff is at point $M$ with coordinates $a$, $b$, and
$c$ in the $x$, $y$, and $z$ directions respectively then the
difference between the result for $(0,0,0)$ and the result for
$(0,0,9)$ will depend only on $c$ because $a$ and $b$ are
included in the total distance for both results .
For example if
was
,
would be
and
would be
, or rather
R
is greater than
and the difference between them is
, which means that M is
(half of
) above the middle at
For example if $\hspace{2mm}c\hspace{2mm}$ was
$\hspace{2mm}7$,$\hspace{5mm}R(0,0,0)\hspace{5mm}$ would be
$\hspace{5mm}a+b+7\hspace{5mm}$ and
$\hspace{5mm}R(0,0,9)\hspace{5mm}$ would be
$\hspace{5mm}a+b+(9-7)\hspace{5mm}$, or rather
$\hspace{5mm}a+b+2\hspace{5mm}$\par R$(0,0,0)$ is greater than
$R(0,0,9) $and the difference between them is $5$, which means
that M is $2.5$ (half of $5$) above the middle at $4.5$
In general $c$ is half of (R$(0,0,0) - $R$(0,0,9) + 9)$
The same logic can be used to find $a$ and $b$:
$a$ is half of $(R(0,0,0) - R(9,0,0) + 9)$
$b$ is half of $(R(0,0,0) - R(0,9,0) + 9)$
So the four results $R(0,0,0)$, $R(9,0,0)$, $R(0,9,0)$ and
$R(0,0,9)$ are enough to locate the target.
Do you think you could find the
metagiff in less than 4 moves?
If so, how, and will it work in all cases?