Tony sent us his answers to the first parts.

(a) $6$ units squared ($=3\times 2-0\times 5$)

(b) $12$ units squared ($=3\times 4-2\times 0$)

(c)$9$ units squared ($=4\times 3-1\times 3$)

(d)$10$ units squared ($=2\times 3-4\times -1$)

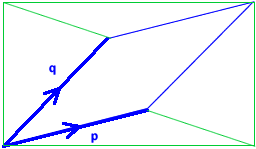
James, Jamie and George from Gillingham School sent us their formula for the area of the general parallelogram.

$a d-b c$.

Here's one way to work that out.

Parallelogram with rectangle and extra lines

Remember that

p = (\begin{matrix} a \\ b \end{matrix})

and

q = (\begin{matrix} c \\ d \end{matrix})

The diagram shows the parallelogram inside a rectangle with base $a + c$ and height $b + d$ . This rectangle has area $(a + c) (b + d)$ . If we could find the areas of the triangles outside the parallelogram, then we could subtract them from the area of the rectangle to find the area of the parallelogram.

The bottom triangle has height $b$ and base $a + c$ , so has area $\frac{1}{2} b (a + c)$ .

The triangle on the right has (if you imagine it on its side so that its base is at the bottom) height $c$ and base $b + d$ , so has area $\frac{1}{2} c (b + d)$ .

The triangle at the top is congruent to the triangle at the bottom (it has been rotated by $180^{\circ}$ ), so has area $\frac{1}{2} b (a + c)$ .

The triangle on the left is congruent to the triangle on the right, so has area $\frac{1}{2} c (b + d)$ .

So the area of the parallelogram is

$(a + c) (b + d) - 2 \times \frac{1}{2} b (a + c) - 2 \times \frac{1}{2} c (b + d) = a b + b c + a d + c d - a b - b c - b c - c d = a d - b c$ ,

just as James, Jamie and George said.