About 15 years ago I had to suddenly do some maths with some 10 year old boys who were a bit turned off about Maths. If it had been today in England they would have said "It's not Cool!!!" There were two small PE hoops nearby and some small bean bags. I put down the hoops as you see:-

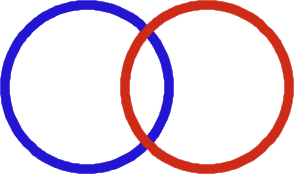
I collected 8 of the Bean Bags - "do they really have beans in?" I asked, they did not know and neither did I. Never mind. I suggested that we put them in the hoops. Four ended up being in the blue hoop, 6 in the red hoop so that two were in the over-lap. We went on to talk about how many were in the blue and how many were in the red and how, the ones in the middle seemed to be counted twice. Try this for yourself.

We tried putting the bean bags about in the hoops in a different way and each time we counted how many were in each of the two hoops.

Well it was time to use the yellow hoop that had been around.

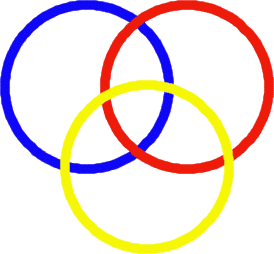
I suggested we made sure that there were 4 in the blue, 5 in the red and 6 in the yellow. So we all tried and then. . . . . . . . . . . .?

Well have a go at this one.

This month's investigation is to take this much further. Try to find as many ways as you can for having those numbers [ 4, 5, 6, ] using just 8 objects. I guess you'll need to record your results somehow so that you do not do the same ones twice!

Have you found yourself using some kind of "system" or "method" for going from one arrangement to the next. Try to explain it if you have.

When you're pretty sure you cannot find any more, check yours with a friend and see if there are any new ones!

As always we then have to ask "I wonder what would happen if. . . ?"

This month it's very easy to invent new ideas. "I wonder what would happen if I used a different number of objects?" - you could go about this in order and try 6 objects and then 7, you've done 8 so move onto 9. . . . .

Any other ideas?

What about this one?

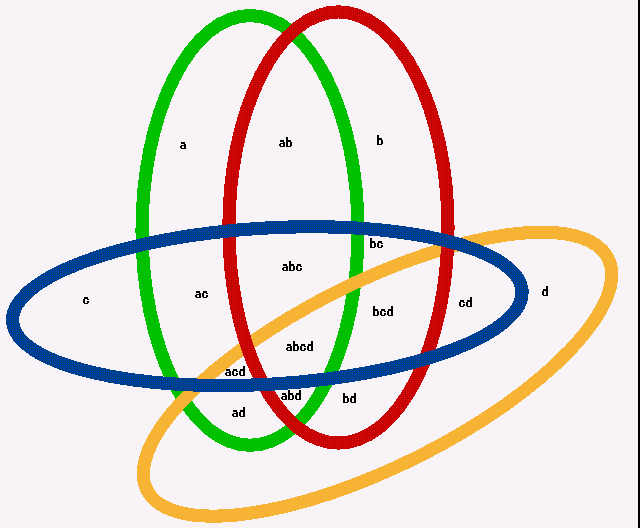
I've given a label to each part - otherwise it gets confusing - "VERY CONFUSING!"

What about using 8 objects and 3, 4, 5 & 6 for the four hoops?

Have a go.

If that's just too much then go back to the 3 rings and ask a question about using a different set of three numbers for the three hoops.
Do the three numbers have to be different?
Are there any interesting patterns or relationships in the results showing how many ways you can do each question?

"I wonder what would happen if . . . ?"

Talk about it with others!