Whirling Fibonacci squares
Image
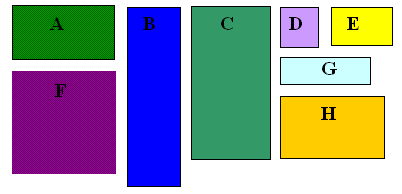
| Which of these rectangles are the same shape? Can you find pairs of the same shape?
How can you be sure that they are exactly the same shape and not just nearly the same shape? The colours give a clue but there is a mathematical property here that you can use to test if two rectangles are the same shape.
Can you work out what that property is? |
Two rectangles are the same shape if one is an enlargement of the other. You can test them by finding the ratio of the length of the long side divided by the length of the short side.
For example F and D are squares and the shape ratio is 1.
The long thin rectangles B and G have shape ratio 3.5 and rectangles A and C have shape ratio 2.
Rectangles E and H are golden rectangles and they have a shape ratio which is called the golden ratio, for which the symbol $\phi$ is often used. We are going to find out more about $\phi$.
The Fibonacci sequence 1, 1, 2, 3, 5, 8,13, 21, 34, 55, ... is defined by the rule that you start with the first two terms 1, 1 and add two successive terms in the sequence to get the next term. The rule for this sequence can be written as a formula with $F_n$ for the $n^{th}$ Fibonacci number: $F_n = F_{n-1}+ F_{n-2}$, with the first two terms: $F_1=1, F_2=1.$
What does the Fibonacci sequence have to do with golden rectangles and the golden ratio? The following activity shows the connections.
Image
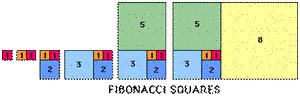
| As in this diagram, draw two squares of unit area side by side on a piece of squared paper, then a square of side 2 units to make a 3 by 2 rectangle, then a square of side 3 units to make a 5 by 3 rectangle, and continue drawing squares whose sides are given by the Fibonacci numbers until you fill your piece of paper. |
We call these 'whirling squares' because they spiral round and round. Try to draw as many squares as you can on your sheet of paper by carefully positioning the first two squares. Now imagine that the paper extends for ever in all directions and the process continues indefinitely. What happens to the shapes of the rectangles?
Look at the rectangles in your 'whirling squares' diagram: 1 by 1, 2 by 1, 3 by 2, 5 by 3, 8 by 5 ... and so on. You will see that the ratios of the long side to the short side of the rectangles, given by the ratio of successive Fibonacci numbers, starts off as $${1\over 1}=1, {2\over 1}=2, {3\over 2}=1.5, {5\over 3} = 1.666.., {8\over 5}=1.6,....\mbox{ and so on}$$ Now use a calculator and work out the next ten ratios. What do you notice?
Now you can experiment using a spreadsheet. This will be handy if you don't have a calculator, and if you have worked the ratios out for yourself the spreadsheet will enable you to discover more.
Image
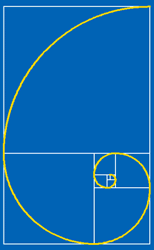
| OK, if you have explored the ratios using the spreadsheet you have some pretty convincing evidence that the ratio of successive terms of the Fibonacci sequence tends to the limit called the golden ratio which has a value $\phi \approx 1.618$.This is a fact but we have not proved it yet.
Now you might like to draw this spiral for yourself on the whirling squares diagram you have already drawn. Just draw the curve from corner to corner across each square. |
