Links to the University of Cambridge website
 Links to the NRICH website Home page
Links to the NRICH website Home page

 Links to the NRICH website Home page
Links to the NRICH website Home page

Nurturing young mathematicians: teacher webinars
30 April (Primary), 1 May (Secondary)
30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Journeying in Numberland
Age 7 to 11
Challenge Level 





- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
Journeys in Numberland
Tom and Ben are in Numberland in the district called Addition.
They have a map which looks like this:
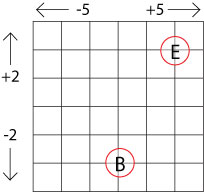
They are at point B and they begin their journey with ten points.
For every square they walk to the right on the map, they add five.
For every square they walk to the left on the map, they take away five.
If they go North (up on the map), they add two for every square, and if they go South (down on the map), they take away two for every square.
First they make these journeys:
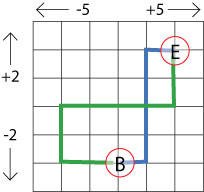
The blue line shows Tom's journey and the green line shows Ben's.
How many points do they have each when they reach E?
Do you notice anything?
Here is a different grid for you to make up some journeys of your own, beginning at B and ending at E.
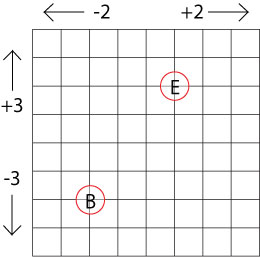
You can download and print off this sheet which has two copies of the grid map.
What do you notice about your different journeys?
Can you explain your observations?
After they had explored in the district called Addition in Numberland, Tom and Ben go on to the district called Multiply.
Here they have a new map which looks like this (here are two copies of the map):
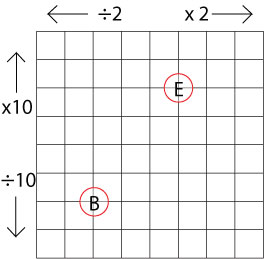
They explore here too. Each time they start at B with $10$ points and make their way to E. Try lots of journeys yourself.
What do you notice about the journeys this time?
Can you explain why this happens?
Why do this problem?
This problem will give learners a chance to make predictions and generalisations. It also provides practice in simple addition and subtraction, and later in multiplication and division. It draws out the inverse relationship between the pairs of operations but it also encourages children to think about the order of operations.
You will need copies of this sheet, and for the second part of the problem this sheet. Squared paper might also be useful.
Possible approach
You could start by showing the first part of the problem to the whole group and by explaining the setting for the problem. A small scale version could be drawn out on the playground or on the hall floor so that the game can be played practically. The first 'journeys' of both boys could be worked out at this stage.
After this introduction, the group could work in pairs so that they are they are able to talk through their ideas with a partner, using copies of the first sheet. Encourage them to find interesting routes that use subtraction as well as addition. Routes can be drawn using different colours but pairs may well need more than one copy of the sheet. Children may need to use jottings
to keep track of their calculations and these could be done on paper or mini whiteboards, for example.
Before having a go at the second part of the problem (multiplication and division), encourage pairs to predict what they think might happen. You may feel that calculators could be used for checking results at this stage.
At the end of the lesson, bring the whole group together again to discuss their findings. They could show their most interesting and/or longest routes. Were they surprised by the results? Why do they think this happened? Although this task focuses only on numerical operations, the explanation of the results demands a very sound understanding of the number system.
Key questions
Can you find a more interesting way to go that uses subtraction as well as addition?
Do you notice anything about those answers?
Can you find a more interesting way to go that uses division as well as multiplication?
Would it be a good idea to use a calculator to check those results?
Can you explain your findings?
Possible extension
You could ask learners to find routes which give the smallest or largest possible answer, staying within the grid. Or they could find routes which involve exactly two subtractions, for example. Alternatively, you could challenge some learners to create their own grid on which different routes between the same starting and end points produce different answers. Why does their grid work? (A combined add-subtract and multiply-divide grid leads to the need for brackets.)
Possible support
Some children might benefit from starting on the Stage 1 version of this problem: The Add and Take-away Path.You may also like
Counting Counters
Take a counter and surround it by a ring of other counters that MUST touch two others. How many are needed?
Cuisenaire Squares
These squares have been made from Cuisenaire rods. Can you describe the pattern? What would the next square look like?
Consecutive Numbers
An investigation involving adding and subtracting sets of consecutive numbers. Lots to find out, lots to explore.