 Links to the NRICH website Home page
Links to the NRICH website Home page

30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Walk and Ride



- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
This was a tough one, but several people took on the challenge! The answer 'about 7 miles' is a good answer, but three people managed to be even more exact.
The first step is to work out how far the students have walked by the time the car reaches the school.
Syed (Foxford School and Community College) explains:
"The car travels to school at a speed of 40 miles an hour.
The 5 students walked at a speed of 4 miles an hour.
So the car will take an hour to arrive at the school.
At the same time, the 5 students would have just done a 4 mile
walk.
The distance between the school/car and the 5 students should now
be
40 - 4 = 36 miles."
So the next step is find out when the returning car and the students will meet, and so find how much further the students will have walked. This is where people started thinking differently! See if you can follow their thinking.....
George (Rosebank Primary School, Leeds) says "If the car goes back 20 miles the students will be two miles nearer. Now there is fourteen miles between the car and the other five students. The teacher drives ten miles more and the students walk one mile. This time there is 3 miles between them. The students walk three elevenths of a mile and the car gets there exactly at the same time. I think the answer is that they meet at the seventh mile and three elevenths of a mile. " (This comes out as 7.27)
Thomas (Tattingstone School) says, "I worked this out by giving the distance the students walked a letter, in this case "L". I then worked out that however far the students walked, the car had gone ten times further. By the time the car had driven 5 students back to school, the other students had walked 4 miles. The rest of the distance that had to be travelled was 36 miles. Because the car goes ten times as far as the students, the number of L's to be travelled was 11. Then I worked out the number of 11's in 36, which was 3.27272727, rounded off and added to 4 which brought me to 7.27."
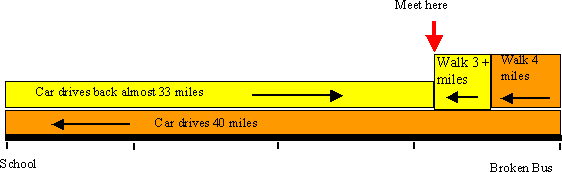
(George and Syed sent in similar diagrams to this. Drawings like this can be very helpful for working out problems)
Syed (Foxford School and Community College)
"The car then travelled at a speed of 40 miles an hour towards the students while at the same time the students are walking at a speed of 4 miles an hour. We have to find out how much distance the 5 students have to walk to be able to meet the car while the car is travelling.
All we have to do is to convert the speeds like this:
Car = A/B = 40 miles/an hour
5 students = C/D = 4 miles/an hour
We have to convert the two speeds so that A + C = 36, because this
is the distance between them, and so that B = D, because it must
take the car and the 5 students the same amount of time to be able
to travel to the part where they meet.
Car = 40 miles/an hour = 40 miles/60 minutes = about
33 miles/50 minutes
5 students = 4 miles/an hour = 4 miles/an hour = about
3 miles/50 minutes
33 + 3 = 36 miles
50 = 50" (This means the student walked about 4 + 3 = 7 miles)
Jessica (Tattingstone School) found another approach (with just a little help) to working out the 'bit more' the students might walk before the car arrived.
"......the teacher only has to drive back 36 miles but as she is travelling her 36 miles the students are still walking along at 4 miles per hour, making a combined speed of 44 miles per hur and they only have to travel 36 miles.
At 4 mph = 4/44 x 36 = 3.27 miles
At 40 mph = 40/44 x 36 = 32.73 miles
(Note: 3.27 + 32.73 = 36 miles)
So the students have walked (another) 3.27 by the time the car
reaches them".
You may also like
Great Squares
Investigate how this pattern of squares continues. You could measure lengths, areas and angles.
Rope Mat
How many centimetres of rope will I need to make another mat just like the one I have here?
A Rod and a Pole
A lady has a steel rod and a wooden pole and she knows the length of each. How can she measure out an 8 unit piece of pole?