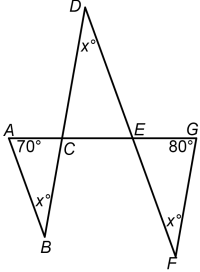
Alternate angles BDF and DFG are equal, so lines BD and FG are parallel.
Therefore angle BCA = angle FGC = $80^{\circ}$ (corresponding angles).

Consider triangle ABC: $x + 70 + 80 = 180$ so $x=30$.  

Alternatively, note that angle ACB = angle DCE, and therefore triangles ABC and CDE are similar, so angle DEC = $70^{\circ}$. Similarly, angle DCE is $80^{\circ}$, and therefore $x=30^{\circ}$.