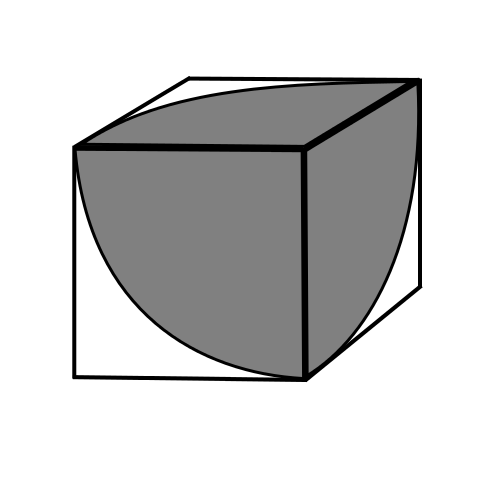In one hour, the snail can reach points within 1m of the corner at which it starts. So it can reach some of the points on the three faces which meet at that corner, but none of the points on the other three faces.

On each of the three reachable faces, the points which the snail can reach form a quarter of a circle of radius 1m.

So the required fraction is $\frac{3 \times \frac{1}{4}\pi \times 1 \times 1}{6 \times 1 \times 1} = \frac{\pi}{8}$.