Start with a $10$ by $10$ grid.

If you cut out each corner square, it could be folded into an open-top box that had an $8$ by $8$ base and was $1$ square deep. That means that the box would be able to hold $64$ cubes.

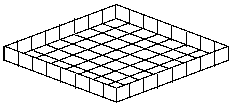
What size square should you cut out of each corner to make the box that would hold the greatest number of unit cubes?

(Another way to ask this question is 'Which box has the greatest volume of space available?'.)