In this article, I will outline suggestions for tasks which will help young children develop the concept of fractions. 

Halving
Let's start by sharing into two parts.  Let me describe an activity I have used many times and find to be quite successful (see Paper Halving):

I have often started by presenting pupils with A4 sheets of paper and encouraging them to halve each piece in different ways.
If the pupils are sitting in groups of four or five then I would set them the challenge of producing four or five different ways of halving.
They would have to be able to say how they know that each pair of halves is equal.

If you try this you may get examples like these where A and B show the halves, whether they are single or separate parts:



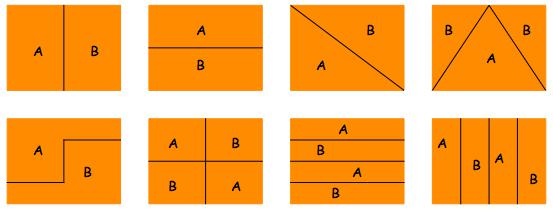
When that has been thoroughly explored and talked about, I would go on to other sizes of paper (see What Do You See Here?). I would find many different sizes of paper, postage stamp size up to A3, and ask learners to halve them. Then I would gather the halved pieces and the whole ones together. I would announce to the children that here were some of the paper sizes we had seen with a “half” piece put by its side. The children, seated in a big circle on the floor discuss and share ideas, and I have found they said things like, ”Here is the green sheet and its half”.

So it all looked like this but on a very large scale:


After a while I would remind them that they had all spoken about halves, and yet these halves were different. On one occasion, it was at this point that Janet said, “It's just that each piece has its own parts!”.

Other children who seemed confident in producing most of the first eight shown above and others like them, were then prompted by me to consider curves as well as straight lines.

This led to results like these:


Why not have a go at exploring halving paper with your pupils?

Having done so, it would be a good opportunity to have a look at the NRICH activity Halving.  Then, before leaving halving, have a look at Happy Halving that goes from rectangles to more irregular shapes.

Thirds and quarters
Having halved then let's proceed to thirds and then quarters. It seems that most would go from halves to quarters probably halving and halving again. But for those who have mastered halving well, moving to thirds is a good challenge. There seems to be a variety of ways in which, as adults, we would third a sheet of A4. Some will often start loosely folding into a “Z” shape and 'shuffle' it around until the three parts are equal:


Others may fold from one side until the edge 'halves' the remaining part:


So, we can invite pupils to split their new A4 sheets into three and ask them to explain how they know their thirds are the same size. This has the potential for being a catalyst for a lot of thinking and discussion, which can give you an insight into how the pupils are thinking about fractions and/or area.

Going further
Before we leave sharing A4 sheets I have found it very valuable for pupils to be challenged with more unusual sharing situations. For example, giving a group of five pupils nine sheets of A4 to share between them. Quite often I have found that halving is the dominant feature here. It goes something like this:

The nine sheets are shared one at a time to each pupil and so there are four A4 sheets left.
The four sheets are then halved giving eight halves. These are shared leaving three halves.
The three halves are then halved giving six quarters. These are shared leaving one quarter.
The one quarter is halved giving two eighths - and they notice that's not enough!
The two eighths are halved giving four sixteenths - again, not enough.
The four sixteenths are then halved giving eight thirty-seconds (that always seem to sound strange!).
There are enough of these to share one each leaving three thirty-seconds left.
The three thirty-seconds are halved giving six sixty-fourths.
These are shared and so there is one sixty-fourth left.

Now comes the surprise. They take a pair of scissors cut that sixty-fourth (which is about the size of a postage stamp) and, as if it's quite natural, they cut that sixty-fourth into five pieces!  It's just so surprising that they then cut the postage stamp sized paper into parts to match the number of pupils sharing as if it's just the normal thing to do.

Some pupils may be able to name some of the small fractions that they came across when describing what each pupil has now got. i.e. one whole, one half, one quarter, one thirty-second and one sixty-fourth. The final part is one fifth of one sixty-fourth.

I have found that after they have done two or three more of these kinds of problems they have a discussion and then decide that they could simply (in the above case) cut each of the eight A4s into five pieces giving each pupil eight one fifths each. They can then get to see more easily that eight shared among five is eight fifths. Some will probably go on to see that as one whole and three fifths each. 

I remember well the excitement one child had over this discovery and came up to me and said “I can do any of these sharings in my head, ask me one”. Of course when I said things like thirteen shared among seven she would quickly reply, “Thirteen sevenths!”.  Other children went on to repeat that kind of answer and then say, "That's one and six sevenths!”.

Some re-inforcement of these beginning concepts in fractions can be carried out by using long narrow strips of paper. (I have got hold of 'till rolls' for this purpose.) According to the practical space you have available you give the pupils each a measured length of paper, for example approximately 4 metres. I used to have very many of the same lengths available so that the pupils can carry out many experiments. I also made sure that there were many measuring devices freely available (tape measures, rulers, metre sticks etc.).  I used to give them a few challenges and them allow them to suggest new challenges for themselves. So I would ask questions like, “If your 4 metre length has to be shared among seven of you, what length would you have each?".

Discrete materials
So far the sharing into parts has been with continuous material and we now come to discrete material - counters, cubes etc. I believe it is very useful to start with some simple sharing situations with counters/cubes. Give every pupil something like 24 cubes and ask them to share them equally among various numbers of people. It is important also to allow a lot of discussion so that pupils can raise questions about what they find out and for them to be able to ask questions as well.  Pupils should be encouraged to think about the sharing that produces some counters/cubes left over. At some stage there will probably be a need to explore what to do with these 'left-overs'.   I remember, on one occasion, quickly getting some biscuits to use in place of counters/cubes. The pupil I was working with was sharing 25 among three people. The left over biscuit was quite easily seen as something you could share among three.  A Bowl of Fruit is a suitable activity to engage the pupils at this stage.

In conclusion
Many situations in and around the classroom, and beyond, require sharing to take place and pupils' journeys of 'fraction discovery' will vary.  However, it is good if we can journey with them.

You may like to take a good look at this YouTube video which shows two children working on a difficult sharing situation practically, sharing eight sausages among five people with a teacher who questions appropriately to get the thinking going.