Links to the University of Cambridge website
 Links to the NRICH website Home page
Links to the NRICH website Home page

 Links to the NRICH website Home page
Links to the NRICH website Home page

Nurturing young mathematicians: teacher webinars
30 April (Primary), 1 May (Secondary)
30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Mathsjam Jars
Age 14 to 16
Challenge Level 





- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
Well done to Anurag and Christina for their
solutions to this problem:
The seven letters that take the same time to fill up are: I,L,O,E,M,T and H, all with a volume $14$cm$^3$ and thus taking $14$ minutes to fill.
The letter S takes the longest to fill up ($14.5$cm$^3$, $14.5$ minutes to fill).
The letter V fills up first ($13$cm$^3$, $13$ minutes to fill).
The letter A will take $13.5$ minutes to fill.
The graph corresponds to the letter M. Some points in the graph are over measured, for instance, the points between 4 and 5 cm.
The seven letters that take the same time to fill up are: I,L,O,E,M,T and H, all with a volume $14$cm$^3$ and thus taking $14$ minutes to fill.
The letter S takes the longest to fill up ($14.5$cm$^3$, $14.5$ minutes to fill).
The letter V fills up first ($13$cm$^3$, $13$ minutes to fill).
The letter A will take $13.5$ minutes to fill.
The graph corresponds to the letter M. Some points in the graph are over measured, for instance, the points between 4 and 5 cm.

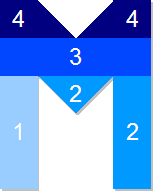
1. 0 - 3 minutes - filling one
'leg' of M, with rate of height increase constant due to constant
width
2. 3 - 7 minutes - further water
will run over in to the central dip of the M, and then once this is
filled into the opposite leg. These have a combined volume of
$4$cm$^3$ and so take 4 minutes to fill
3. 7 - 11 minutes - water fills top
rectangular section with constant rate of height increase
4. 11 - 14 minutes - filling up top
two trapezoidal sections of M
5. 14 - 16 minutes - letter
completely full - no further height gain
Section 4 in the period 11-14 minutes should actually be
represented by a curved line on the chart as the width of the
section being filled is changing with height, and therefore so will
the rate of height increase.