Quadrilaterals

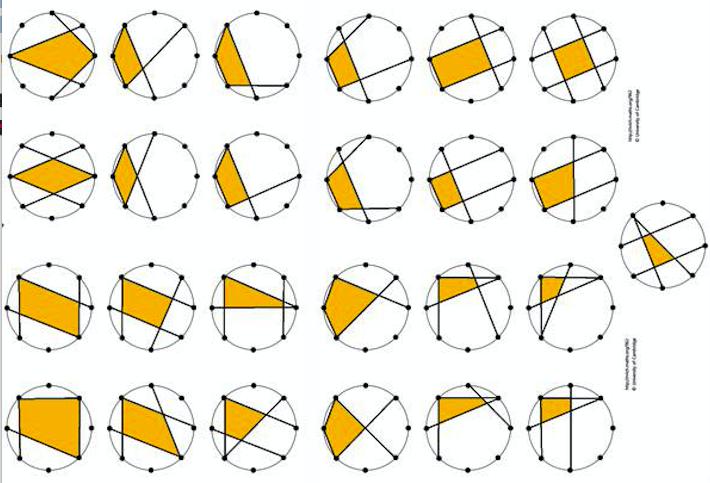
This problem can have more than one solution, depending on what you decide 'different' means. Thomas, Lydia and Bethan from Old Earth Primary School described a quadrilateral by the number of dots you move around the circle as you join its four corners. For example, a 1115 quadrilateral would look like this:

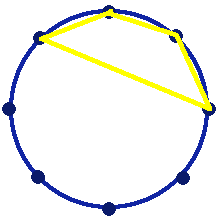
They thought there were eight different possible quadrilaterals although they didn't explain exactly how they found them. This way of recording the quadrilaterals is very useful - a good idea! Here is the list of eight that Thomas, Lydia and Bethan found:

trapezium -1115
trapezium -1214
trapezium -1232
kite -1133
rectangle -1313
square - 2222
other scalene quadrilaterals - 1223 and 1124

Some children at Breckland Middle School also worked on this problem. They said:

We found ten solutions to this problem. To make sure there were no repeats, we cut them all out and compared them in pairs, then in tables and then as a class. Only one of each shape remained (reflections are allowed!).

Here is a picture of the solutions they found:

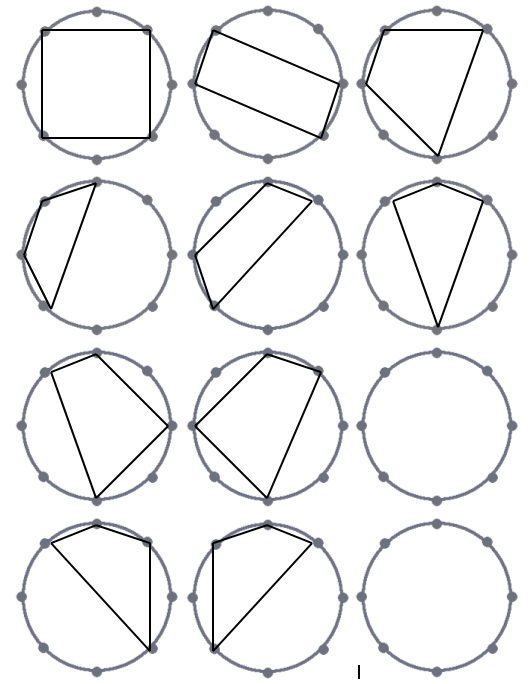
It is interesting now to compare these two sets of solutions. Can you match Thomas, Lydia and Bethan's solutions to the pictures above? So, if we decide that 'different' means that one shape cannot fit on another, even if it is rotated, then there would be ten as children at Breckland have drawn.

But, if we decide that reflections are the same too, then I think there are eight, as Thomas, Lydia and Bethan suggest. Here is a picture of the eight that Thomas, Lydia and Bethan found but I have drawn them in a particular order to make sure I didn't miss any out. Can you see what my system was?

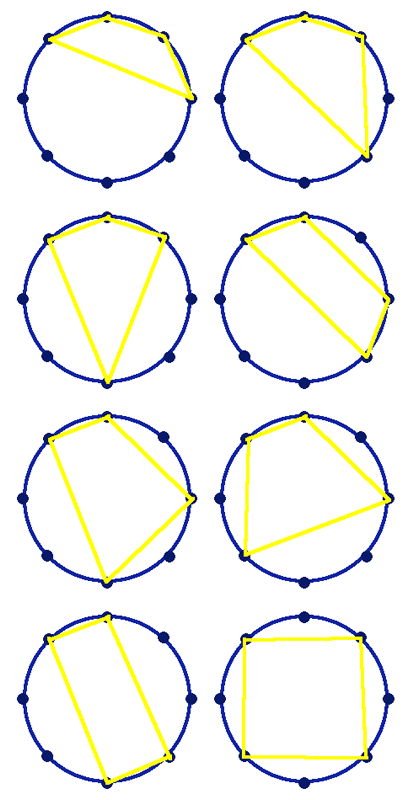
If we define 'different' in one of the ways above, the problem is quite manageable. Some of you made life very challenging by opening up the possibilities. Kerim, working at home, and Maiya, from Marist College, approached the problem differently. Kerim wrote:

I figured this out by first labelling each point with a letter; A, B, C, D, E, F, G and H.
I started listing the shapes possible with two points that were sitting close together. I started with H, A and found five combinations with H, A, B shapes; four combinations with H, A, C shapes; three combinations with H, A, D; two combinations with H, A, E and one combination with H, A, F.
My shapes looked like this:

HABC
HABD
HABF
HABF
HABG
HACD
HACE
HACF
HACG
HADE
HADF
HADG
HAEF
HAEG
HAFG

This was my stage 1. For stage 2 I moved to another line that had points next to each other. A and B. My first set of combinations had only 4 possibilities because I had already created one of the other shapes in the first stage. I realised that I could follow the same pattern of each set of possibilities having one less shape. This looked like:

ABCD
ABCE
ABCF
ABCG
ABDE
ABDF
ABDG
ABEF
ABEG
ABFG

At this point, I knew that it was unnecessary to list the shapes as I worked around the circle. I knew that the next stage would have one less set of combinations, and that the highest set would have one less than the highest number of possibilities in my last stage. I wrote down the numbers 3, 2, 1 for the next stage, and then 2 and 1 and finally just 1. I added the number of all of these possibilities together. I did it twice to make sure I didn't make a mistake. I had thirty five.

So, Kerim found thirty-five quadrilaterals which all have two corners next to each other. She then began to think about quadrilaterals where none of the corners was immediately next to another on the circle. She says:

I knew that I could also draw a square not using points next to each other. I had discovered this when I was first experimenting with the problem. I could make two different squares this way. I played around with the circle and could not come up with any more quadrilaterals that didn't have two points next each other. I added these 2 squares to my 35 and got 37. I sure hope I'm right. I offered my dad a dollar if he could come up with more, but he has not met my challenge! Thanks for the problem. It was fun to solve.

Kerim has been very systematic in the way she has listed the quadrilaterals, which is very helpful. If you've had a go at this problem, how did you think about 'different' quadrilaterals? Do you agree with what Kerim has found? It is interesting that Kerim said she thought about the square because she'd played around with the problem to start with. It might be that using a combination of drawings and other ways of describing the quadrilaterals (eg using numbers or letters) works well for this problem.