Copyright © University of Cambridge. All rights reserved.
'Quadratic Rotation' printed from https://nrich.maths.org/
Show menu
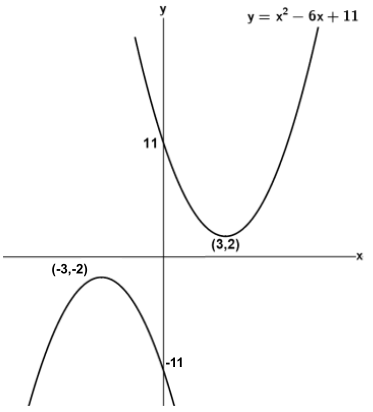
Answer: $y=-x^{2} - 6x - 11 $, which is the same as $y= -(x + 3)^{2} - 2$.
Completing the square
New graph is a negative quadratic with maximum $(-3,-2)$
The curve hasn't changed shape so $y=-x^2+...$ (not $y=-2x^2+...$ etc)
$\therefore$ equation is $y=-(x+3)^2-2$
Comparing coefficients
New graph has equation $y=ax^2+bx+c$
The curve hasn't changed shape but the quadratic is negative so $a=-1$
Intercept is $-11\Rightarrow c=-11$
$y=-x^2+bx-11$
And $(-3,-2)$ is on the graph so
$-2=-(-3)^2+b(-3)-11\\
\Rightarrow -2=-9-3b-11\\
\Rightarrow 18=-3b\\
\Rightarrow b=-6$
So the equation is $y=-x^2-6x-11$
Using $-x$ and $-y$
Rotation of $180^\circ$ about $(0,0)$ is the same as swapping $x$ for $-x$ and $y$ for $-y$
Swap $x$ for $-x$ and $y$ for $-y$ in the equation $y=x^2-6x+11:$
$$\begin{align} -y&=(-x)^2-6(-x)+11\\
\Rightarrow -y&=x^2+6x+11\\
\Rightarrow y&=-x^2-6x-11\end{align}$$
This problem is taken from the UKMT Mathematical Challenges.
You can find more short problems, arranged by curriculum topic, in our short problems collection.