Monday tablecloth

Well done to Joseph and Dylan from Wilson's Grammer School and Joe from Leventhorpe. Each found a pattern which they then investigated to find a general formula. 

Start with the example below, where the solid grey line is the line of symmetry. The red square forces the square symmetrically opposite to also be red. 

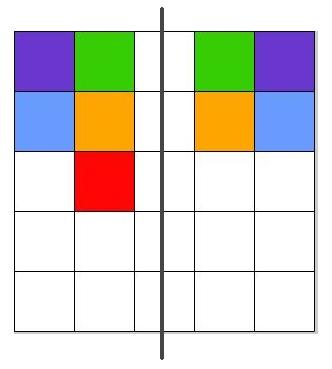
So the squares on one side of the line of symmetry determine the colours on the other side. 

The squares with different colours to each other form a rectangle of size $n \times d$, where $n$ is the number of rows in the tablecloth and $d$ is the number of columns with different colours (including the squares on the line of symmetry). 

Komal from India illustrated this pattern by writing each colour as a different pronumeral: 

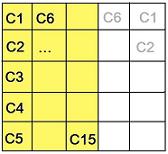
Observe that the orange section (squares with unique colours) has area  $15=5\times 3 =5\times \frac{5+1}{2}$ 

So $d=\frac{n+1}{2}$,  and the maximum number of colours for 1 line of symmetry is  $n \times \frac{n+1}{2}$

 

Tuesday tablecloth

The squares with unique colours form a rectangle of area $x\times y$ in one quadrant of the tablecloth, plus the colour in the central square (shaded in orange).

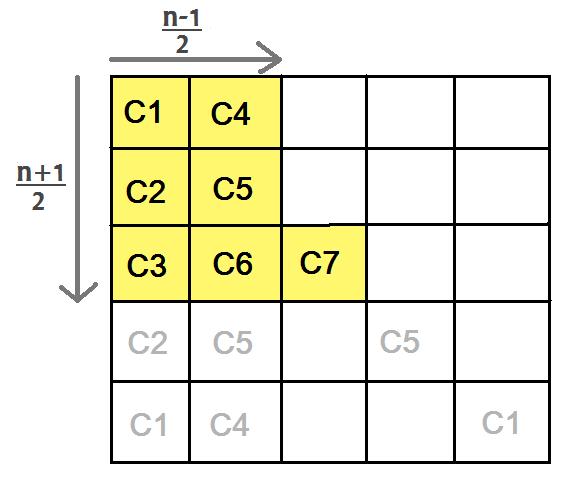
In the $5\times5$ case, the area of this rectangle is $6=3\times 2 = \frac{5+1}{2} \times (\frac {5+1}{2} -1) $.

So the maximum number of colours in this rectangle is $\frac{n+1}{2} \times (\frac{n+1}{2}-1)=\frac{n+1}{2} \times \frac{n-1}{2}$. 

Adding in the central square, the maximum number of colours is  $\frac{n+1}{2} \times \frac{n-1}{2} + 1$

 

Another explanation, using the rotational symmetry of order $4$, was given by Nathan, Jack, Joseph, Harry and Daren from Wilson's Grammar School.

Except for the central square, each colour appears $4$ times in the tablecloth due to the rotational symmetry of order $4$. So excluding the central square, the number of colours is $\frac{n^2-1}{4}$

Adding in the colour C7, the maximum number of colours is thus $\frac{n^2-1}{4}+1$

 

Wednesday tablecloth

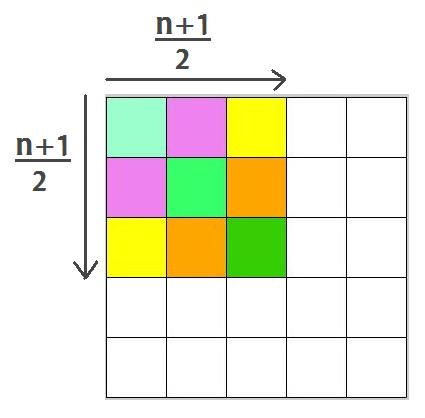
The number of different colours in each tablecloth is a square number, say $d^2$. Since $d$ is the length of a quadrant (including the squares on the line of symmetry) we have $d=\frac{n+1}{2}$.

 

So the maximum number of colours is  $(\frac{n+1}{2})^2$

 

Thursday tablecloth

In the $5\times 5$ case the maximum number of different colours is $9$. 

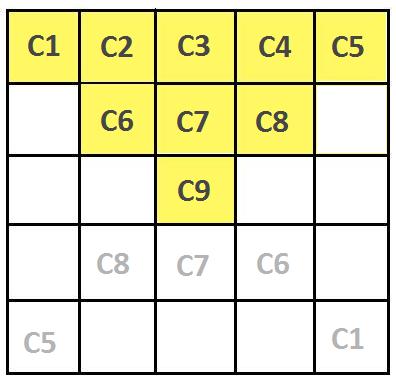
From the diagram above, the orange section (squares with unique colours) has area $9=1+3+5$. 

Recall that the sum of consecutive odd numbers is $1+3+5+...+(2k-1)=k^2$. Noting that $5=2\times3-1$, we then get $9=3\times3=(\frac{5+1}{2})^2$

 

So the maximum number of colours is $(\frac{n+1}{2})^2$

 

Are you able to predict this result? Compare the types of symmetries of this tablecloth with the Wednesday tablecloth; why is the formula for the number of colours the same?

Friday tablecloth

In the $5\times 5$ case the maximum number of different colours is $6$.

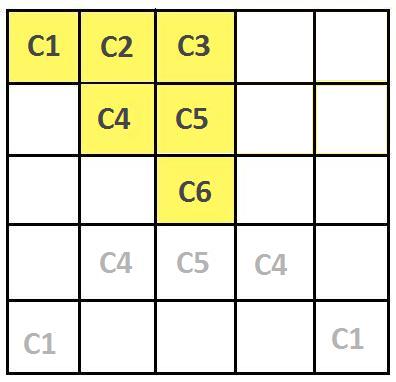
From the diagram above, the orange section (squares with unique colours) has area $6=1+2+3$.

Recall that the sum of consecutive numbers is $1+2+3+...+k=\frac{k(k+1)}{2}$, and by writing the area in terms of $n=5$,  we get $6=3\times \frac{3+1}{2}=\frac{5+1}{2} \times \frac{\frac{5+1}{2}+1}{2}$

 

So the maximum number of colours is  $(\frac{n+1}{2})^2\times \frac{\frac{n+1}{2}+1}{2}=\frac{(n+1)(n+3)}{8}$

 

Well done to Joe and Komal who also thought about what would happen if $n$ were even, and to Karrar from Michaela Community School who considered how to write an nth term rule which covered both the odd and even cases in one formula.