 Links to the NRICH website Home page
Links to the NRICH website Home page

30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Cubic Conundrum



- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
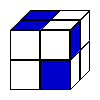
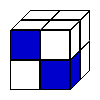
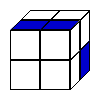
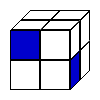
The solution below has the cubes in this slightly different order:
 |
 |
 |
 |
 |
 |
Correct solutions to the first part of the question were received from: Alastair H (Forres Academy), Andrei L (School 205, Bucharest). The solution below is based on Andrei's submission. Well done to both of you.
First I created a small cube from the net in the figure and observed the cubes from the problem:
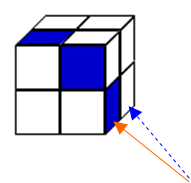
The first cube cannot be formed from that net, because the square marked with a red arrow should be in the position marked with a blue arrow:
Looking at the cube made from the net: It is possible to see that the second cube (horizontally) can be made from that net and also the last three
In conclusion, the 4 cubes denominated before are the same one, created from the net (B, D, E and F below).
The second part of the problem:
First shade the three faces of the view B of the cube which are not visible. Then do the same with the other three views of the same cube (D,E and F).

A  B
B  C
C  D
D  E
E  F
F
You end up shading all the faces. This means that you can see all the faces of the cube in the four views B, D, E and F so there are no hidden faces where you can shade additional sections.
You may also like
Presents
We need to wrap up this cube-shaped present, remembering that we can have no overlaps. What shapes can you find to use?
Platonic Planet
Glarsynost lives on a planet whose shape is that of a perfect regular dodecahedron. Can you describe the shortest journey she can make to ensure that she will see every part of the planet?
Face Painting
You want to make each of the 5 Platonic solids and colour the faces so that, in every case, no two faces which meet along an edge have the same colour.