Tri-split

A point P is selected anywhere inside an equilateral triangle. What can you say about the sum of the perpendicular distances from P to the sides of the triangle? Can you prove your conjecture?

Areas and Ratios

What is the area of the quadrilateral APOQ? Working on the building blocks will give you some insights that may help you to work it out.

Six Discs

Six circular discs are packed in different-shaped boxes so that the discs touch their neighbours and the sides of the box. Can you put the boxes in order according to the areas of their bases?

Crescents and Triangles

Stage: 4 Challenge Level:

The trick with this question was not to make life difficult by working values out. As a consequence some of you managed much more elegant solutions than others. Here is an example based on that offered by Shu Cao (very well done). Jeongmin Lee, Rebecca Bartram (The Mount School, York) and Andrei Lazanu (School 205, Bucharest) should also be congratulated.

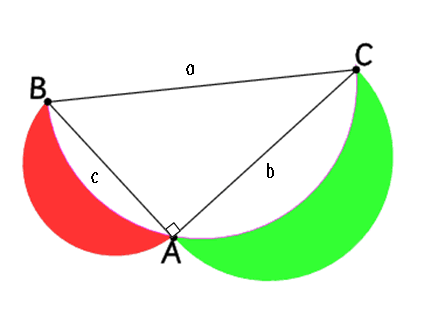
Using Pythagoras` theorem in $ABC$,

$$\begin{eqnarray}a &=& \sqrt{b^2 + c^2} \\ \mbox{Area of semicircle on BC} &=& \pi \frac {a^2}{4}\\ &=& S1\\ \mbox{Area of semicircle on AC} &=& \pi \frac {b^2}{4}\\ &=& S2 \\ \mbox{Area of semicircle on AB} &=& \pi \frac{c^2}{4}\\ &=& S3\\ \mbox{Area of crescents} &=& S2 + S3 + \mbox{Area ABC} - S1\\ &=& \pi \frac {b^2}{4} +\pi \frac {c^2}{4} + \mbox{Area ABC} - \pi \frac {a^2}{4}\\ &=& \pi \frac {b^2}{4} + \pi \frac{c^2}{4} - \pi \frac {a^2}{4} + \mbox{Area ABC}\\ &=& \frac{\pi}{4} \times ( b^2 + c^2 - a^2 ) + \mbox{Area ABC}\\ &=& 0 + \mbox{Area ABC} \\ &=& \mbox{Area ABC} \end{eqnarray}$$

Cresents duiagram

Inscribed circle. Right angled triangles. Pythagoras' theorem. Circles. Tangents. Investigations. Visualising. Dynamic geometry. Circle theorems. Area.

You may also like

Tri-split

Areas and Ratios

Six Discs

Crescents and Triangles

Stage: 4 Challenge Level: