Triangular tantaliser
Problem
Here is a 4 by 4 dotty grid:
How many different triangles can you draw by joining dots on the grid?
We count two triangles as the same if you can cut one out and fit it exactly on top of the other.
Can you come up with a convincing argument that you have found all the possible triangles?
Getting Started
Is there a systematic way that you could work that would ensure you don't miss any triangles?
You could start with certain limitations (constraints) and exhaust all possibilities - try to justfy how you know there are no other triangles in this "category".
Then extend your investigation to more categories.
Student Solutions
Several pupils from The Mount School in York attempted this problem. Two pupils began to try to explain how they knew they had found all the solutions. They said:
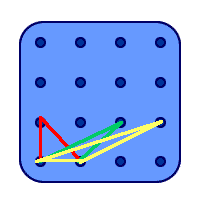
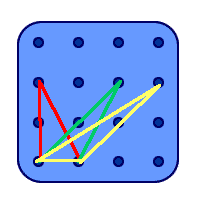
"If you've got a base of 1 unit and a height of 1 unit then there are 3 triangles possible,
if you've a base of 1 and a height of 2 then there are another 3 possible triangles and
a base of 1 with a height of 3 gives another 3.
So you've got 9 triangles with a base of 1"
Here are two diagrams to illustrate this:
Image
|
Image
|
This is a good and convincing start - they made 27 triangles but do not appear to have considered triangles whose bases are not horizontal.
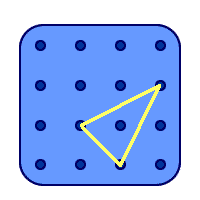
Can anyone develop these excellent beginnings? Perhaps the students at The Mount School could put their ideas together to come up with a more "complete" solution.
Teachers' Resources
Here is an interactive environment that you could use with your students to record their findings:
You might need to show more than one triangle on each diagram.
Here is a printable sheet you might like to use.