Just Rolling Round

P is a point on the circumference of a circle radius r which rolls, without slipping, inside a circle of radius 2r. What is the locus of P?

The coke machine in college takes 50 pence pieces. It also takes a certain foreign coin of traditional design. Coins inserted into the machine slide down a chute into the machine and a drink is duly released. How many more revolutions does the foreign coin make over the 50 pence piece going down the chute? N.B. A 50 pence piece is a 7 sided polygon ABCDEFG with rounded edges, obtained by replacing AB with arc centred at E and radius EA; replacing BC with arc centred at F radius FB ...etc..

Rotating Triangle

What happens to the perimeter of triangle ABC as the two smaller circles change size and roll around inside the bigger circle?

Tilting Triangles

Stage: 4 Challenge Level:

Some excellent ideas and approaches to this problem. The first part of the problem (when the triangle is larger than the square) is fairly accessible; as is the part where the two equal sides of the triangle shrink to less than half the length of the side of the square but the bit in between is tricky!!

The first solution offered below is based on the work of Thomas Davies, Hannah McKenzie, Elliot Husband, Lizzie Farnham and Hannah Bradley of Madras college The group also spent time looking at what happens as the triangle shrinks (not so easy). Well done to all of you.

The second solution is from Andrei Lazanu of School 205, Bucharest. Thank you for this Andrei

Other excellent solutions were received from Alison Colvin, Sheila Norrie and Shona Leenhouts, also of Madras College, who have partly answered one of the January problems (if you tackle this problem you can refer to what you did for tilting triangles). I think the January version is a little easier.

Solution one

Introduction

We believed that the triangle took up a quarter of the square, and that a total of four triangles could fit around the square. We created a moving example:

Explanation

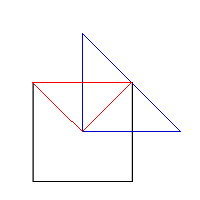
We started by rotating a square inside the four triangles as this has the same effect as rotatiing the triangle (editors note:I "liked this bit of lateral thinking").

From our "moving" representation (Fig. 1) we could see that it is always possible to fit four right angled triangles around the centre of the square. This is because the centre of the square allows a 360° rotation and, as the traingles are right angled, they have angles of 90° (360 / 90 = 4).

Fig 1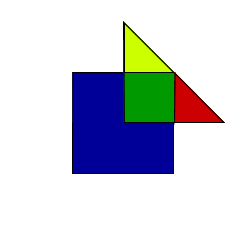

Fig 2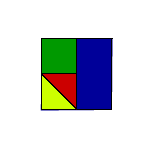

Fig 3

We believed that a quarter of the square was overlapped by each triangle and we set out to prove this.

First we placed the triangle in a simple position on the square (Fig. 2). We could clearly see that the green area of the triangle is a quarter of the square - and what about the yellow and red areas...?

We suspected that they added up to another quarter. To show this we cut out the areas and stuck them on to the square (Fig. 3). This showed that the yellow and green areas also took up a quarter of the square and the the whole triangle took up half the square.

We soon realised that this was only an example for one position of the triangle - we needed to look at the bigger picture.

The Bigger Picture

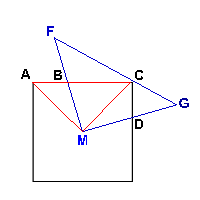
As can be seen the square in the middle of the four triangles is 2 units by 2 units. This means that the overlap of each of the four triangles is congruent and makes up a quarter of the square.

Fig 4

As the four triangles fit on the square at all times the overlap of the triangles onto the square must always be a quarter of the square which is equal to 1 square unit.

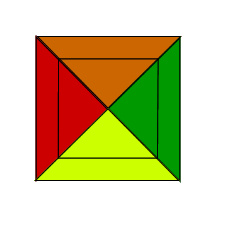
Conclusion

In our write up we have shown that 4 triangles can fit around the square and that the area of overlap is 1 square unit. This is always true as long as the sides of the triangle are 2 units.

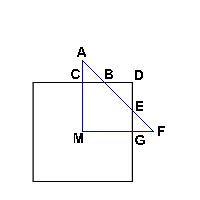
The Second Solution

To find the length of the diagonal of a square of side 2, using the Pythagorean Theorem:

$2^2 + 2^2 = d^2$

So, $d = 2\sqrt{2}$.

1. Starting with the triangle with the two equal sides 2 units in length. \par

1a) If the hypotenuse of the isosceles triangle is parallel to one side of the square.

This means the equal sides of the isosceles triangle are on the diagonal of the square; the area of the square occupied by the triangle is the area of the right-angled isosceles triangle, of side half the diagonal.

This means that half the diagonal is $\sqrt{2}$ units. The area of the triangle is $$ \frac{1}{2} \times 2\sqrt{2} \times 2\sqrt{2} = C $$ 1b) The triangle is in a tilted position.

Triangles $AMB$ and $CMD$ are congruent, because they are formed by the rotation of triangle $FMG$. This means their areas are equal. So, the area of the square occupied by the triangle is the same. Any position could be reduced to position a).

1c) The equal sides of the triangle are parallel to the sides of the square.

It is very clear that the triangle forms in the square a smaller square of area 1 unit$^2$.

2. The congruent sides of the triangle are $\sqrt{2}$ units.

2a) The hypotenuse of the isosceles triangle is parallel to one side of the square.

As seen from 1a, this is a particular case. The hypotenuse of this triangle is the side of the square, also having the same area as in 1a.

2b) The triangle has a tilted position.

In this part of the problem, the area of the square covered by the triangle is smaller than 1 unit$^2$.

2c) The equal sides are parallel to the sides of the square.

Triangles $ACB$ and $AGF$ are both isosceles right-angled triangles, with equal sides of $\sqrt{2} - 1$ units because they are right-angled triangles with $45^{\circ}$ angle. So, $BDE$ is also a right-angled triangle with the congruent sides:

$1 - (\sqrt{2}-1) = 2 - \sqrt{2}$

The area of the polygon $BCMGE$ is the area of quadrilateral $DCMG$ minus the area of triangle $BDE$. This is:

$1 - [((2 - \sqrt{2})2)/2] = 1 - [(4 + 2 - 4\sqrt{2})/2] = 1 - (3 - 2\sqrt{2}) = 2\sqrt{2} - 2$ units$^2$

3. Here, I must find the limit where the area of the triangle is all inside the square. This happens when triangle $MAF$ is the same as triangle $MCG$. This happens when the congruent sides of the right-angled isosceles triangle are 1 unit. If I reduce further the side of the triangle, all the triangle will be inside the square.

Complex numbers. Games. Real world. Visualising. Pythagoras' theorem. Mathematical reasoning & proof. Circles. Working systematically. Interactivities. Making and proving conjectures.

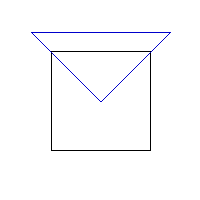
You may also like