 Links to the NRICH website Home page
Links to the NRICH website Home page

30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Arclets



- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
I received two superb solutions from Sheila Norrie, Shona Leenhouts and Alison Colvin, and Sarah Gibbs, Kathryn Husband and Gordon Ducan from Madras College, St. Andrews. It is so difficult to do justice to them before our publication date for this month. I will try to work on them over the next couple of weeks and publish them, or at least a flavour of them next month. Well done to all of you. A solution based on the one received from Andrei Lazanu from School 205, Bucharest, Romania is used below - but do watch this space next month!
First, I looked at the figure with four nodes. The node is formed from $2/4$ of a circle, and the arc connecting two nodes of $1/4$ of a circle.
The perimeter of this arclet is: $$4\pi \times \left(\frac{2}{4} + \frac{1}{4}\right) = 4 \pi \times \frac{3}{4} = 3\pi$$
Looking at the figure with three nodes, I observe the same pattern: the node contains $2/3$ of a circle, and the arc connecting two nodes $1/3$. The perimeter of the figure is: $$3\pi \times \left(\frac{2}{3} + \frac{1}{3}\right) = 3\pi$$
The circumference of a circle of radius $r$ being $2\pi r$, the perimeter ($R$) is in this case $6\pi r$.
For $n = 4$, each node has at the end half a circle, and $4$ quarters join them. So, there are in total $3$ circles, with the same perimeter as before.
Now, I observed a pattern:
The node contains $2/n$ of a circle, and the arc connecting two nodes $1/n$. The perimeter of the figure is: $$n\pi \times \frac{3}{n} = 3\pi$$
When $n$ is very large the figure is very close to a circle. The radius of this circle is $3r$ (three times the radius of the circle whose arcs form the figure with "nodes",. from which the big figure is formed).
This radius of the circle circumscribed to the figure is same for any n. In fact, it is rather difficult to prove this, and I saw it first for $n = 4$, where it could be observed directly that $R$ is formed by $3$ small radii, and then for large $n$. Maybe it would be necessary to use induction!.
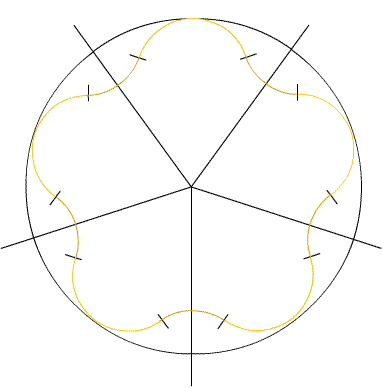
Then I tested the formula I obtained for $n= 5$.
As I know that the figure stays inside a circle of radius $3r$, is it easy to draw it.
Each node has at the end an arc of radius $r$, and of angle $144^{\circ}$. The obtained figure is below.
See also:
This article on Arclets
You may also like
Ladder and Cube
A 1 metre cube has one face on the ground and one face against a wall. A 4 metre ladder leans against the wall and just touches the cube. How high is the top of the ladder above the ground?
Bendy Quad
Four rods are hinged at their ends to form a convex quadrilateral. Investigate the different shapes that the quadrilateral can take. Be patient this problem may be slow to load.