Sending and receiving cards
Problem
There are many festivals and celebrations when we send cards to each other. Some schools organise a postal service within the school and some of the pupils get the job of being postmen/women.
Groups of children send cards to each other sometimes and that's really good for them all; it's a good feeling getting the cards.
Suppose there are three children, Georgie, Jo and Chris, and these three are really good friends. They decide to send cards to each other.
Georgie sends two cards, one to Jo and one to Chris.
Jo sends two cards, one to Georgie and one to Chris.
Chris sends two cards, one to Jo and one to Georgie.


So these three friends send six cards altogether. Also they get six cards altogether!!!!
What if in another class in that school there is a group of four children who are best friends and at this time of the year each sends the others a card.
Raj sends $3$ cards, one to Bex, one to Jon and one to Loo.
Bex sends $3$ cards, one to Raj, one to Jon and one to Loo.
Jon sends $3$ cards....
Loo sends $3$ cards....
So a lot more cards are sent by the four children altogether.
This season's challenge is to explore the number of cards that are sent altogether when there are $5$ children, then $6$, then $7$, etc. , up to perhaps a class of $30$ children who all send cards to each other and you work out how many cards are sent altogether.
Once you have this set of numbers it might be good to write them down underneath one another (a bit like you may have done when you did the investigation called Exploring Wild & Wonderful Number Patterns ).
You could now, if you have not done it already, start looking at some of the things that pop up in this number pattern. I'm not sure what they all are of course, but I've seen a few patterns, so get searching for what YOU can find!
Then you'll be able to ask, "I wonder what would happen if I ...?'' about so many things.
Getting Started
How will keep track of the number of children you have tried?
Student Solutions
We received many good quality solutions this month. A lovely Christmas present for us! We haven't included all of them, but instead we've chosen a variety of solution types to show you. Thank you to Robert, Sarah and Anna for your correct and well-presented solutions.
From The Juniors: The Christian School (Takeley)
Michael: "To find the number of cards you have to times the number of people by the number of cards they sent.''
Class: "The number of cards sent is one less than the number of people.''
Our Table:
| Number of people |
Number of cards sent |
| 1 | 0 |
| 2 | 2 |
| 3 | 6 |
| 4 | 12 |
| 5 | 20 |
| 6 | 30 |
| 7 | 42 |
| 8 | 56 |
| 9 | 72 |
| 10 | 90 |
| 11 | 110 |
| 12 | 132 |
Frances: "They are all even numbers.''
Lawrie: "The units digit goes 0, 2, 6, 2, 0, 0, 2, 6, 2, 0''
Michael: "The units digits are symmetrical in the table''
Class: "Let's carry on the number pattern:''
0, 2, 6, 12, 20, 30, 42, 56, 72, 90, 110, 132, 156, 182, 210, 240, 272, 306, 342, 380, 420, 462, 506, 552, 600, 650,...
Lawrie: "The units digit repeats the pattern every five numbers.0, 2, 6, 2, 0''
David - with help from the class and much amazement:
"Every time there is a six you add one more ten to the tens column.''
30 3+1=4
42 4+1=5
56 5+2=7 You've hit the six so you add one more ten
72 7+2=9
90 9+2=11
110 11+2=13
132 13+2=15
156 15+3=18 You've hit the six so you add one more ten
182 18+3=21
210 21+3=24 etc
It does carry on.
Class: "While we were working on last month's dice problem (a bit late) we saw the pattern of triangular numbers and were playing around with squares and doubling the triangular numbers in order to find some patterns etc when:''
Samuel: "All the numbers in the card problem are double the triangle numbers!''
NB Sam is our Mr Memory Man.
Thank you for such an enjoyable problem. My class think you make things look easy and it's your fault that they get so complicated. Apparently you work some kind of magic Bernard!
Siobhan of West Flegg Middle School sent the following solution:
| "4 x 3 = 12 |
| 5 x 4 = 20 |
| 6 x 5 = 30 |
| 7 x 6 = 42 |
| 8 x 7 = 56 |
| 9 x 8 = 72 |
| 10 x 9 = 90 |
| 11 x 10 = 110 |
| 12 x 11 = 132 |
| 13 x 12 = 156 |
| 14 x 13 = 172 |
| 15 x 14 = 210 |
| 16 x 15 = 260 |
| 17 x 16 = 272 |
| 18 x 17 = 306 |
| 19 x 18 = 342 |
| 20 x 19 = 380 |
| 21 x 20 = 440 |
| 22 x 21 = 462 |
| 23 x 22 = 506 |
| 24 x 23 = 552 |
| 25 x 24 = 600 |
| 26 x 25 = 650 |
| 27 x 26 = 702 |
| 28 x 27 = 756 |
| 29 x 28 = 812 |
| 30 x 29 = 870 |
I worked out all of this because I wanted to find out if there was any pattern in the last numbers. I found out that there was. The pattern is 2, 6, 2, 0, 0 and it carries on about 6 times. Anyway, I found out that the whole class would send to each other all together 870 cards. I worked out the sum by doing this:
| 30 |
| x29 |
| --- |
| 270 |
|
600
|
| --- |
|
870
|
| === |
But, what if two of the friends fell out with each other?
What if they changed to a new school?
What if nearly all the class started to hate each other?
What if one of the children sent a card to the teacher?
Would any of these ifs change the sequence of the numbers at the end?''
Natasha of West Felff Middle School says:
"Jenny sends 4 cards: 1 to Paula, 1 to Sarah, 1 to Roxy, 1 to
Hannah
Paula sends 4 cards: 1 to Jenny, 1 to Sarah, 1 to Roxy, 1 to
Hannah
Sarah sends 4 cards: 1 to Jenny, 1 to Paula, 1 to Roxy, 1 to
Hannah
Roxy sends 4 cards......
Hannah sends 4 cards....
Therefore with a group of 5 children, 20 cards are sent
altogether
Steph sends 5 cards: 1 to Emma, 1 to Laura, 1 to Gemma, 1 to
June, 1 to Becky
Emma sends 5 cards: 1 to Steph, 1 to Laura, 1 to Gemma, 1 to June,
1 to Becky
Laura sends 5 cards......
Gemma sends 5 cards......
June sends 5 cards.......
Becky sends 5 cards......
Therefore with a group of 6 children 30 cards are sent.
''
Natasha continued using this method, then followed the pattern all the way up to 30 children, as shown below:
"Here are the final numbers of what I have done above, but up to 30 children:
| 5 children: 20 cards | The first digits of these numbers go from 2-5 |
| 6 children: 30 cards | |
| 7 children: 42 cards | |
| 8 children: 56 cards | |
| 9 children: 72 cards | The first digits go from 7-15, so they are jumping in twos |
| 10 children: 90 cards | |
| 11 children: 110 cards | |
| 12 children: 132 cards | |
| 13 children: 156 cards | |
| 14 children: 182 cards | |
| 15 children: 210 cards | |
| 16 children: 240 cards | There are two 2s, three 3s, two4s, two 5s, two 6s, two 7s and two 8s |
| 17 children: 272 cards | |
| 18 children: 306 cards | |
| 19 children: 342 cards | |
| 20 children: 380 cards | |
| 21 children: 420 cards | |
| 22 children: 462 cards | Every single number is even because they have all got an even number for the last digit |
| 23 children: 506 cards | |
| 24 children: 552 cards | |
| 25 children: 600 cards | |
| 26 children: 650 cards | |
| 27 children: 702 cards | |
| 28 children: 756 cards | |
| 29 children: 812 cards | |
| 30 children: 870 cards'' |
This is part of another solution sent in by Rachel from West Flegg Middle School. It shows another way to solve the problem.
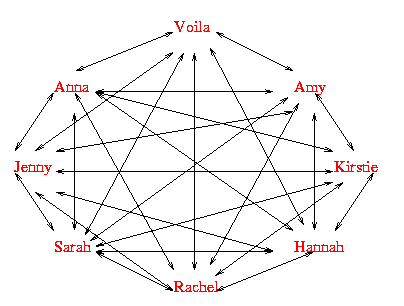
"The number of arrows round the persons name represents how many cards they have sent and received, which is always one number less that the group number.''
Chris used a grid diagram to discover more patterns.




I see a pattern.
On a grid you end up with a diagonal line.
The numbers when multiplied are all even in the totals.
There is a pattern in the last digits of the multiplied numbers.
The pattern is 2, 0, 0, 2, 6, 2, 0, 0, 2, 6...
There is also a pattern where you multiply the number of people (first number) sending the cards by the same number less one (second number) because you don't send a card to yourself.eg:
| 4 | x | 3 | = 12 |
| 1 st = no. of people |
2 nd |
Class of 30 children; 30 x 29 = 870 cards sent.''
Here are results in a spread sheet form;

