Algebraic Fluency of Advanced Students
This brief, informal article reports the results of a short mathematical fluency test administered to students attending the Mathematics Sutton Trust Summer School at Cambridge University.
The purpose of this article was to informally assess the mathematical fluency of students who who might soon be entering their final year of schooling.
The hope of this article is that those involved in university admissions might have a clearer picture of the mathematical fluency of students coming for interview.
The main recommendation arising is that universities make clear to applicants the level of procedural fluency needed for a mathematics course, well in advance so that students have time to practise if necessary.
The questions
The questions were as follows, ordered according to the success rate on the question:
| Question number | Question | Number correct | Number wrong | Number blank | The wrong answers |
| 9 | Write down a decimal between $-0.000345$ and $-0.000354$. | 20 | 0 | 4 | |
| 5 | Evaluate $(-1)^9-(-1)^8$ | 18 | 2 | 4 | $0$ twice |
| 4 | Evaluate $(-0.25) ÷ (-4) -2$. | 17 | 7 | 0 | $-\frac{33}{16}$ $-1.93875$ $1\times \frac{1}{16}$ $-\frac{15}{8}$ $-1$ $\frac{775}{400}$ $-\frac{1}{8}$ |
| 7 | Let A be the set of all even numbers and B the set of all whole number multiples of $3$. Which numbers are contained in both A and B? | 15 | 1 | 8 | |
| 2 | Write down a number between $|102 - 103|$ and $|302 - 300|$ | 14 | 2 | 8 | $1$ $0.5$ |
| 10 | How many solutions $y = 0$ are there to the equation $y = x^{2011}$ where $x$ and $y$ are real numbers? | 13 | 2 | 9 | $2011$ (twice) |
| 8 | Write down a function $f(x)$ which is 'infinite' at $x =-7$ but finite everywhere else. | 11 | 1 | 12 | |
| 6 | Write down the 'infinite n' limit of the sequence $ (7 - (0.25)^n)$. | 6 | 2 | 16 | $6$ $6.75$ |
| 1 | Write down a real valued function of the real numbers which is not constant and always less than $-50$ | 4 | 8 | 12 | $(-50x)^2$ $-x^2-50$ (x3) $\sin(x)$ $-x^2$ (twice) $\ln(x)-50$ |
| 3 | For what range of real numbers x is the following statement true: $(x >2 )^3 > (x > 2)^4$ | 0 | 14 | 10 | Closest 'When $x-2$ is $-1>$ but $<1$ $x<3$ (three times) $x>2$ (twice) $-1x>-1$ |
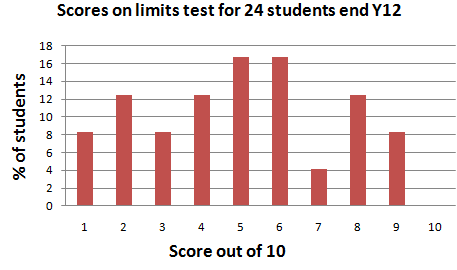
Overall total scores
Background information
In 2011 I was involved in running the academic aspects of the first Mathematics Sutton Trust Summer School at Cambridge University for students interested in applying to university to study mathematics. All 25 students were studying mathematics and further mathematics A-levels, and were selected for the Summer School from a highly competitive set of applicants. They had all completed their first year of 6th form study.
Priority was given to students who met all or most of the following criteria:
- would be the first generation in their family to attend university
- had achieved at least 5 A/A*s at GCSE
- came from neighbourhoods with low overall progression rates to higher education
- attended schools or colleges with a low overall A level (or equivalent) point score
- were under the age of 18 at the time of the summer school
The intention was that applicants were viable as potential university mathematics applicants from disadvantaged backgrounds.
Towards the end of the school when students were comfortable and relaxed I administered a voluntary skills test designed to explore aspects of mathematical fluency such as might be expected in students who might soon be applying to prestigious establishments for university mathematics places. All students volunteered to take the test. The instructions were that the test of 10 questions was only 10 minutes long, students were to start with those questions that seemed easiest and that I was not expecting any students to complete all questions correctly. Students were reassured that this test was anonymous and would have no impact in any way on their application to university.
Interestingly, all students had finished writing before the 10 minutes had passed, informally indicating that they had answered all of the questions that they could and were satisfied with these answers.
http://www.study.cam.ac.uk/undergraduate/access/year12summerschool/
http://www.suttontrust.com/summer-schools/
http://www.suttontrust.com/summer-schools/eligibility/
