Round and Round the Circle printable sheet

I started with a clock without hands or lines showing the minutes (except for those where there is a number). The $12$ was replaced by a $0$ and the numbers placed outside the face.

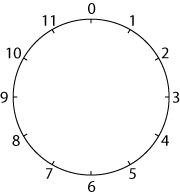
I drew straight lines to join up the numbers.

I started by counting in ones and I got a $12$-gon (that is a $12$-sided polygon - if you like long words you can call it a dodecagon).

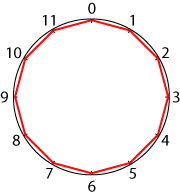
Then I drew straight lines counting round in $2$s. And I got ...?

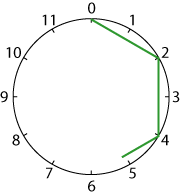
Perhaps you could try without putting the numbers round the circles.

I tried $5$s (wow!) and $6$s (well!).

Each time I go on drawing lines until I get to the point where I first started.

Then I tried $7$s, $8$s, $9$s, $10$s, and $11$s.

Something interesting was happening.

Why don't you try it? What patterns do you notice emerging?

And what about counting round in $12$s?

Which shapes are the same? Can you think of a reason why?

Can you see a connection between the number in which you are counting around the circle and the number of sides in the shape you are making?