 Links to the NRICH website Home page
Links to the NRICH website Home page

30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Are You Kidding



- Problem
- Getting Started
- Student Solutions
An excellent solution from Sheila Norrie of Madras College, who not only managed to find that the area was 48 square units, but was also able to say that there are an infinite number of isosceles triangles with a whole number perimeter and a whole number area. Andrei Lazanu of School 205, Bucharest was also able to establish that the area was 48 square units using a computer program, given below. Both solutions involved exhaustive methods! Well done.
Here is part of Sheila's solution:
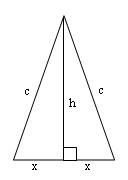 |
We know from Pythagoras theorem that $h^2 + x^2 = c^2$
From this we can say that $c =\sqrt{( h^2 + x^2 )}$
So the perimeter must equal $\sqrt{( h^2 + x^2 )} + \sqrt{(
h^2 + x^2 )} + 2x$
We know the perimeter is 32 so: $$\sqrt{( h^2 + x^2 )} +
\sqrt{( h^2 + x^2 )} + 2x = 32$$ and we know $h = 8$ $$\sqrt{( 8^2
+ x^2 )} + \sqrt{( 8^2 + x^2 )} + 2x = 32$$ $$\sqrt{( 8^2 + x^2 )}
+ x = 16$$
|
To find a solution Sheila then used trial and improvement - testing for values of x from 1 to 6.
If x = 6: $\sqrt{( 8^2 + 6^2 )} + 6 = 16$
x = 6 is the only solution because nothing works for under 6. If x was greater, the perimeter would have to increase which it can't.
We know the area of the triangle = 1/2 bh
For this triangle
- h = 8
- b = 12 (2 x 6)
So area = 48
Part 2
For whole number areas and perimeters, the lengths h, x and c have to be whole numbers. In addition h 2 + x 2 must equal c 2
So we are looking for Pythagorean triples. Since there are an infinite number of Pythagorean triples there must be an infinite number of triangles.
Andrei's program in Matlab that he used to calculate the Pythagorean Triples up to a perimeter of 100 units.
Here is the program:
| Pythagorean Triples i=1; for a=1:100; |
|||||
| a1=a^2; for b=1:100; |
|||||
| b1=b^2; for c=1:100; |
|||||
| c1=c^2; if c1-b1-a1=0 |
|||||
| s=a*b; p=2*(c+a); if p< =100 |
|||||
| v(i,1:5)=[a b c p s]; i=i+1; |
|||||
| end | |||||
| end | |||||
| end | |||||
| end | |||||
| end |