Copyright © University of Cambridge. All rights reserved.
'Approximating Pi' printed from https://nrich.maths.org/
Show menu
A method is to calculate the perimeters or areas of the inscribed and circumscribed polygons to find an upper and lower limit for Pi. I have included a solution from Andrei below based on the perimeter of the two polygons. You could then find the average of the two limits to find an approximation to Pi. As Michael points out Pi is irrational and therefore cannot be calculated exactly. We can still obtain very good approximations to Pi using this method by increasing the number of sides. No one really addressed the issue of the problems with this method, especially for Archimedes as he did not have a calculator or tables to look up roots of numbers. For Archimedes methos of calculating square roots see the problem Archimedes and Numerical Roots.
Andrei's Solution
 |
 |
 |
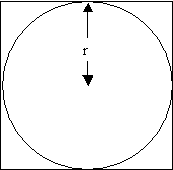
The length of the side of the circumscribed square is $2r$,
where $r$ is the radius of the circle. So, its perimeter is
$8r$.
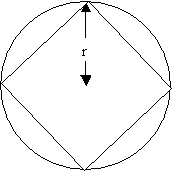
Now, I calculate the length of the inscribed square, using the
Pythagoras Theorem, in a right-angled isosceles triangle, with the
right angle in the centre of the circle, the two congruent sides -
radii of the circle, and the a vertex of the hypotenuses - the side
of the inscribed square:
$2r^2 = l^2$
$l = r\sqrt{2}$
So, the perimeter of the inscribed square is
$4r\sqrt{2}$.
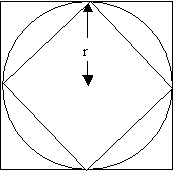
Knowing that the circumference of a circle is $2{\pi}r$, I can
find a minimum and a maximum limit for $p$ from the condition that
the circumference of the circle is lower than the perimeter of the
circumscribed square and higher than the circumference of the
inscribed square:
$4r\sqrt{2} < 2{\pi}r < 8r$
$4\sqrt{2} < 2\pi < 8$
$2\sqrt{2} < \pi < 4$
and approximating $\sqrt{2}$:
$2.8284 < \pi < 4$
Now, I use the same method for the hexagon. First I calculate
the side of the circumscribed hexagon in a right-angled triangle
with one side (the hypotenuses) the line connecting the centre of
the circle with the vertex of the circumscribed hexagon, a side -
half the side of the circumscribed hexagon, and the other - the
radius of the circle. The side of the hexagon is perpendicular on
the radius in the tangency point. The angle between the radius and
the hypotenuses is $30^o$ (Here I use the Pythagoras Theorem and
also the theorem that says than in a right-angled triangle with one
angle of $30^o$, the side opposite to the angle of $30^o$ is 2
times smaller than the hypotenuses): $${ \left({L \over2}\right)^2
+ r^2 = L^2 }$$ $${ {{L^2} \over 4} + r^2 = L^2 }$$ or $${ {3L^2
\over{4}} = r^2 }$$ so, $${ L = {2r \over{\sqrt{3}}}= {{2 \sqrt{3}r
\over{3}}} }$$ The side of the inscribed hexagon is $r$. So, I
found the following inequalities:
$6r < 2\pi r < 6\times (2r\sqrt{3})/3$
$6r < 2\pi r < 4\sqrt{3}r$
$6 < 2\pi < 4\sqrt{3}$
$3 < \pi < 2\sqrt{3}$
and approximating $\sqrt{3}$:
$3 < \pi < 3.4641$