Copyright © University of Cambridge. All rights reserved.
'Sweets in a Box' printed from https://nrich.maths.org/
Show menu
Sweets in a Box printable sheet
A sweet manufacturer has decided to design some gift boxes for a new kind of sweet.
Each box is to contain 36 sweets placed in lines in a single layer in a geometric shape without gaps or fillers.
How many different shaped boxes can you design?
The sweets come in 4 colours, 9 of each colour.
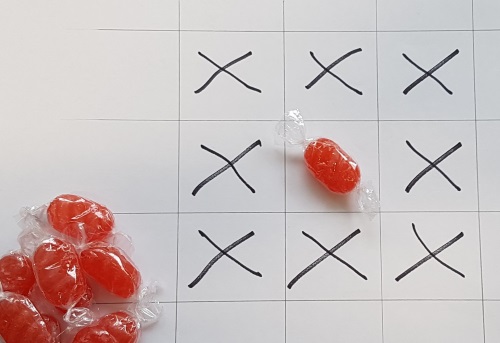
Arrange the sweets so that no sweets of the same colour are adjacent to (that is 'next to') each other in any direction. In the picture below, none of the squares marked x can have a red sweet in them.
Arrange the sweets in some of the boxes you have drawn.
Now try making boxes of 36 sweets in 2, 3 or 4 layers.
Can you arrange the sweets, 9 each of 4 colours, so that none of the same colour are on top of each other as well as not adjacent to each other in any direction?
See if you can invent a good way of showing your arrangement.
Try different numbers of sweets such as 24 or 60 in each box.