 Links to the NRICH website Home page
Links to the NRICH website Home page

30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Kite in a Square



- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
Viola from St George's British International School, Rome in Italy sent in this elegant method:
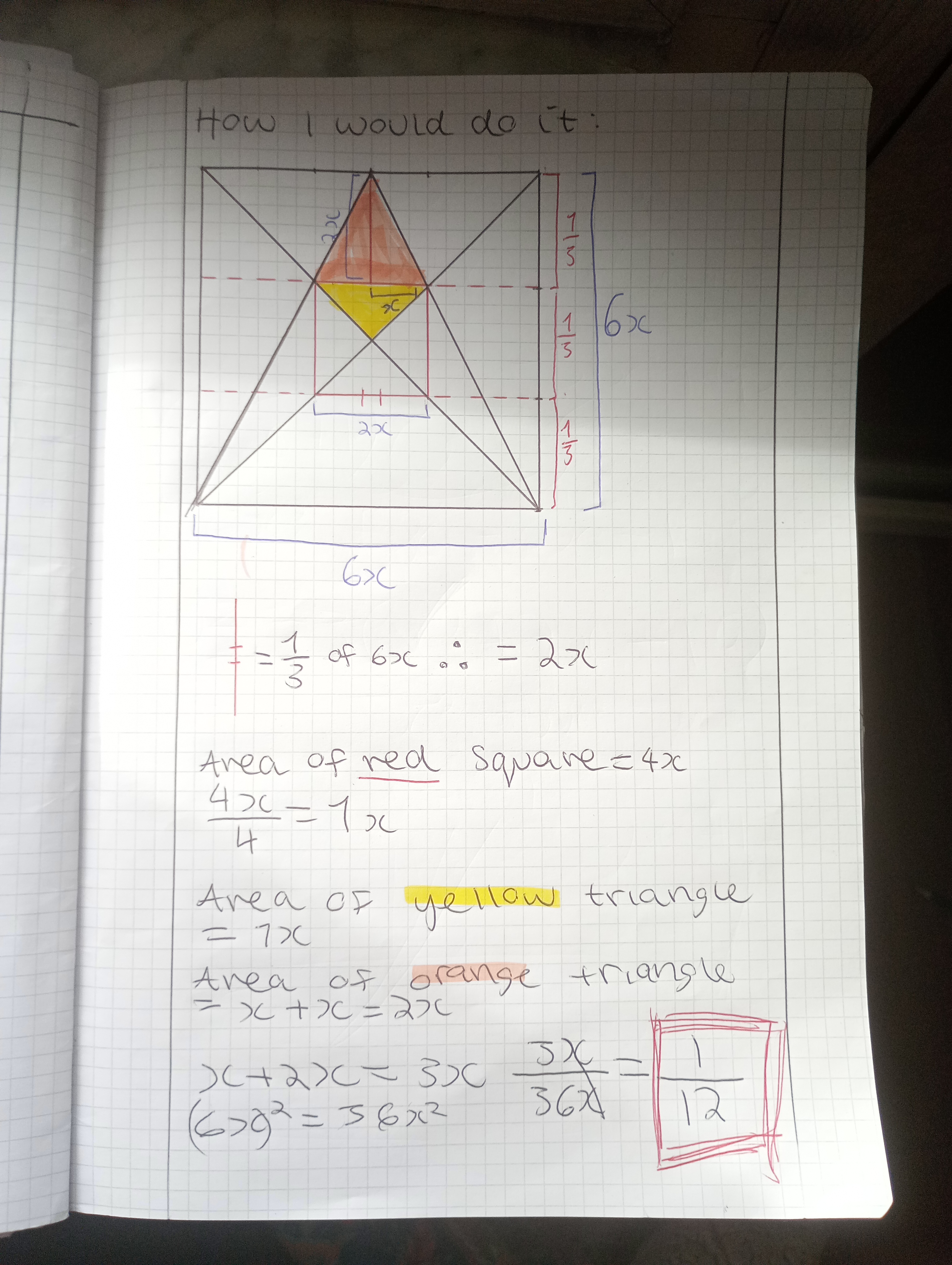
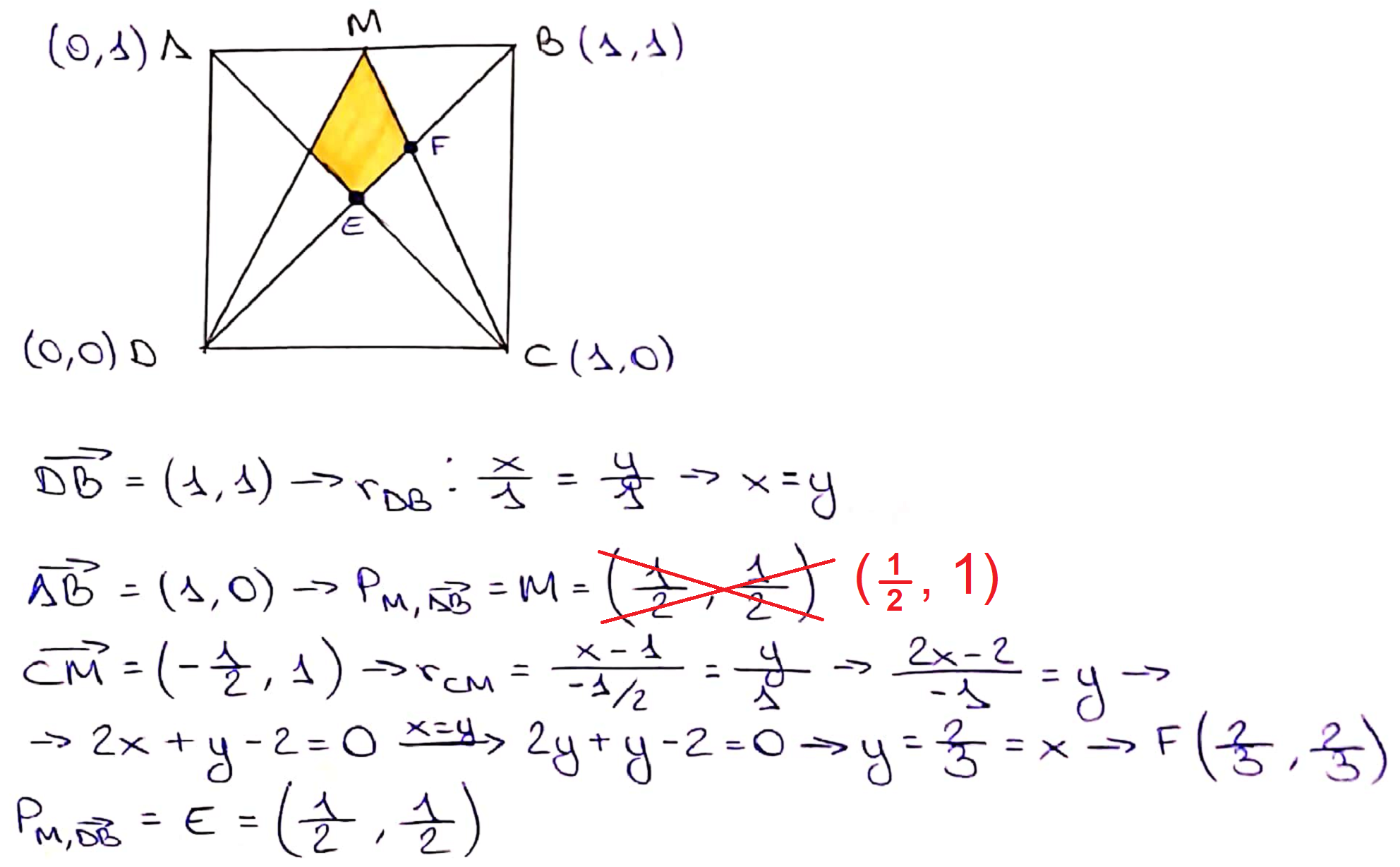
However, Viola has assumed that the vertices of the kite are $\frac12$ and $\frac23$ of the way up the whole square - which might not be true! Zach from Pate's Grammar School in England and Raquel from IES Maximo Laguna in Spain both proved that it is true using coordinates. Below is Raquel's proof that the vertices of the kite are $\frac12$ and $\frac23$ of the way up the whole square:
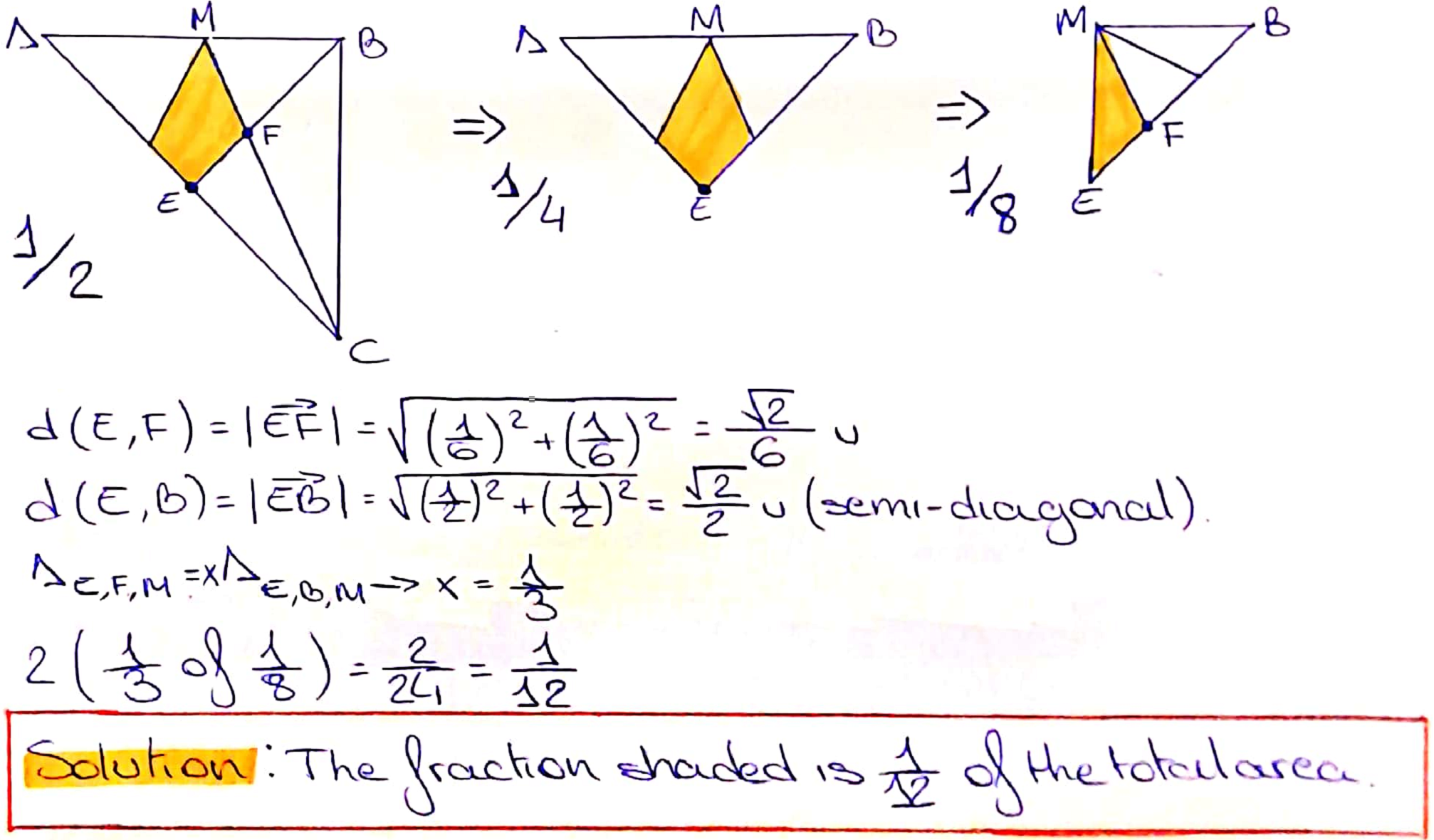
Raquel used this fact to complete a different elegant method:
Zach also used coordinates, but Zach worked with a square with sides 10 units long, instead of 1 unit long. Zach also used a different method. Zach began by defining some lengths as $X, Y$ and $Z$:
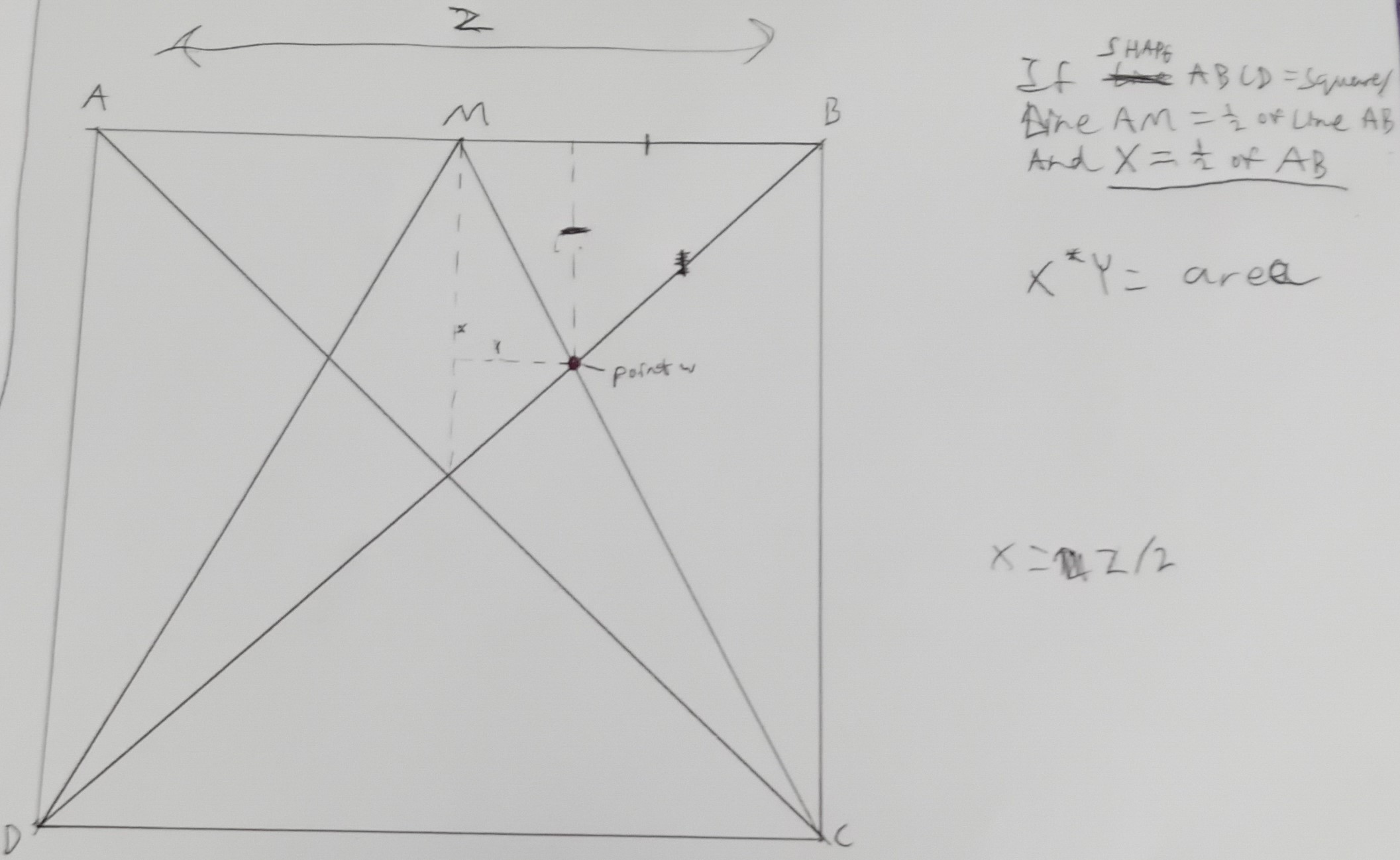
Zach went on to find equations for the lines and line segments. Be careful - sometimes $X$ and $Y$ refer to the coordinates, and sometimes they refer to the lengths defined above.

Rishik K used the three appoaches linked in the problem to compare three different methods. This is Rishik's work:
I enjoyed solving this problem using all the approaches and I believe that they were all smart and interesting methods to work out the shaded area. But I liked the similar figure approach because it was the simplest out of the three and the quote “Mathematics is for lazy people” clearly explains the reason I liked this certain approach.
Pythagoras Approach

Coordinates approach

Similar figures approach
