Links to the University of Cambridge website
 Links to the NRICH website Home page
Links to the NRICH website Home page

 Links to the NRICH website Home page
Links to the NRICH website Home page

Nurturing young mathematicians: teacher webinars
30 April (Primary), 1 May (Secondary)
30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Designing Table Mats
Age 11 to 16
Challenge Level 





- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
I'm going to start by making some basic assumptions:
- The image looks as if it might be life-size, and measuring it I find that the diameter of one rope coil is about 0.5cm, so I'm going to use that as my rope diameter.
- Again measuring from the image, the first part of the rope coil, in the centre of the mat appears to be about 1cm, so I'm going to assume a length of 1cm on the inside of the rope section and 1.5cm on the outside.
- If this is taken as the first horizontal section of rope, then the first vertical section appears to be negligible on the inside of the coil, and two rope diameters on the outside, so 1cm.
- I'm going to assume that all rope sections fit together neatly without any gaps.
- I'm going to also assume that all turns are at 90 degrees.
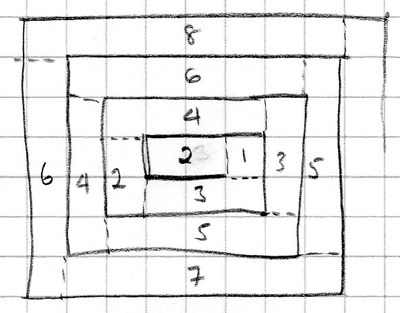 On this basis, I can draw a diagram and start finding the length of rope required for the first few coils of rope.
On this basis, I can draw a diagram and start finding the length of rope required for the first few coils of rope. The squares are 0.5cm x 0.5cm.
The diagram shows me immediately that starting the rope coil like this means that the mat will be longer in one dimension than the other, but is 30cm x 24cm possible?
At this stage, I added dotted lines to my diagram so I could distinguish between horizontal and vertical sections (this could be done in different ways, but provided you do it consistently, exactly how you do it won't matter), and put the number of squares in each section on my diagram.
There appear to be two sequences, one for horizontal sections and one for vertical sections - yours may be different if you have divided your sections up in a different way. Tabulating (in numbers of 0.5cm squares):
| Horizontal strip length | Horizontal length (cm) | Vertical strip length (squares) | Vertical length (cm) | Total length of rope so far (cm) |
|---|---|---|---|---|
| 2 | 1 | 1 | 0.5 | 1.5 |
| 3 | 1.5 | 2 | 1 | 4 |
| 4 | 2 | 3 | 1.5 | 7.5 |
| 5 | 2.5 | 4 | 2 | 12 |
| 6 | 3 | 5 | 2.5 | 17.5 |
| 7 | 3.5 | 6 | 3 | 24 |
| 8 | 4 | 7 | 3.5 | 31.5 |
| 9 | 4.5 | 8 | 4 | 40 |
| 10 | 5 | 9 | 4.5 | 49.5 |
| 11 | 5.5 | 10 | 5 | 60 |
| 12 | 6 | 11 | 5.5 | 71.5 |
The pattern will continue because one square is added to the horizontal or vertical length each time you turn a corner, so 1cm is added for each pair of vertical and horizontal strips.
However, we note that the vertical length is always 0.5cm less than the horizontal length, so 30cm x 24cm will not be possible with this particular way of making the mat.
Revisiting my initial assumptions, clearly the two about perfect fit of rope sections and 90 degree turns are idealisations of the perfect mat. In the real world, there will be gaps between rope sections (indeed, you can see them in the image) and angles will not be exactly 90 degrees. In terms of finding whether a particular size of mat is possible, I think the gaps are probably more significant. The other assumptions depend on these two, of course, but are otherwise reasonable, I think.
The final dimensions of the mat depend on:
- the length of the initial strip before the first turn
- where the coiling stops