 Links to the NRICH website Home page
Links to the NRICH website Home page

30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Getting an Angle



- Problem
- Getting Started
- Student Solutions
This solution is from David Jeffreys
I think I have worked out the answer to getting an angle.
What you do is fold the paper in half (lengthways). Next you fold another so the crease touches a top corner (If you hold it as a landscape) and the corner below it touches the first crease.
The second layer at the bottom corner is 60 degrees. If you want to make it into an equilateral triangle you fold the over side so the fold has the other fold tucked right in and align it up with the other edge.
David supplied some diagrams like the one below.
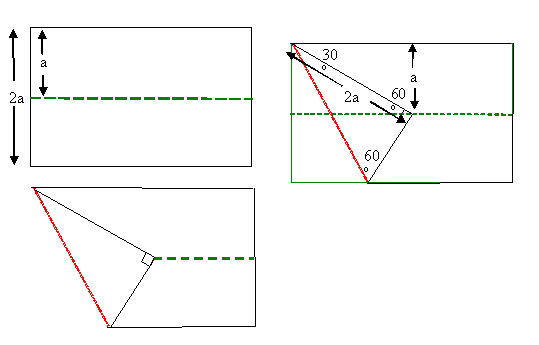
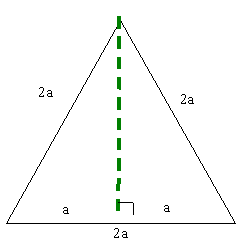
The angles are 30 o and 60 o can be seen if you consider an equilateral triangle of side 2a:
You may also like
Arclets Explained
This article gives an wonderful insight into students working on the Arclets problem that first appeared in the Sept 2002 edition of the NRICH website.
Bow Tie
Show how this pentagonal tile can be used to tile the plane and describe the transformations which map this pentagon to its images in the tiling.
Convex Polygons
Show that among the interior angles of a convex polygon there cannot be more than three acute angles.