 Links to the NRICH website Home page
Links to the NRICH website Home page

30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Three Neighbours



- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
Well done to everybody who found the patterns that happen when we add three consecutive numbers together! We were sent a lot of solutions to this activity.
Dana from Twyford School in England explained why the total is increasing by three each time. You can click on the picture below to enlarge it:
Good explanation, Dana! Instead of thinking about Charlie's method as adding one to each of the numbers, Dana has added three to the smallest number to explain why the total goes up by three each time.
Andy and Rayan from St Mary's Primary in Finchley used some number facts to show why Charlie's method works. This is Andy's work:
Lots of other children also extended Charlie's method to check that it kept going up in threes each time. Well done to Yazan from Dubai International Academy in the UAE, Edward and Leela from Highgate Junior School in the UK, and Sophia, Marie and Amanda from Phorms in Germany for noticing that the answer will always be in the three-times table.
Ava from Highgate spotted another pattern:
Did you know that if you times the middle number by 3 you get the same answer:
10 + 11 + 12 = 33
11 x 3 = 33
Well done for noticing this pattern, Ava! Meyer and Mischa from Highgate, SM, and Eliana from London all noticed this as well. I wonder why this happens?
Lots of the solutions we received explained why the middle number multiplied by three gives the same answer. Sara, Kate, Hailey, Eliza and Raf from the University of Chicago Laboratory Schools in the USA sent in this explanation:
We noticed that the middle number multiplied by 3 is the answer. This is true because if you take 1 from the last number, and add it to the first number, all the numbers will be equal. That means all the answers will be equal to the middle number, there are 3 of them. Therefore, when you add all of the numbers you get the first number times 3, or the middle number 3 times.
Jasper from Highgate Junior School in the UK wrote some number sentences to explain what's happening:
1 + 2 + 3 = 6
(2-1) + 2 + (2+1) = 6
-1 and +1 cross each other out
so, 2 + 2 + 2 = 6
or 2 x 3 = 6
Lots of children explained the pattern using Liz's method, including: Dhruv from St Anne's RC Primary School in the UK; Rafael from Bexley Grammar in the UK; Elijah from St Mary's Primary, Finchley; Nathan from Wilson's School in the UK; Tushar from NPS Rajajinagar in India; Abi from Highgate Junior School; Raif from the UK; Riley from New Cangle Primary School; and Zoya from Halstead Preparatory School. This is Dhruv's work:

Well done to all of you for explaining why the answer is the middle number multiplied by three!
Sunhari from British School Muscat, Casey, Henry and Sofia from Highgate Junior School, Dominique and Cole from Furness Academy, Serena from North London Collegiate, Laura from Plymouth High School for Girls and Rohan and Arnik from Wilson's School used algebra to prove that this will always happen. This is Sunhari's work:
Let the numbers be $n, n+1, n+2$
$$\begin{split} n+n+1+n+2 &= 3n+3\\&= 3(n+1)\\&= 3a\text{ for }a = n+1\end{split}$$
Have a look at Rohan's full solution, which includes diagrams and work on the ideas shown below.
Aadit from Highgate School, Andy, Liam, Kai Yuan and Matthew from St Mary's Primary Finchley and Rafael used a different algebraic method which is very similar to Jasper's method above. This is Aadit's work:
The answer will always be a multiple of $3$ because if the middle number is $n$ then the two other numbers will be $n-1$ and $n+1.$ That becomes $n+ (n - 1) + (n + 1) = 3n.$ The $+1$ and $-1$ cancel each other out leaving $3n.$
Therefore if it is the same as multiplying the middle number by $3,$ it must be a multiple of $3,$ since $3n$ is divisible by $3$ since $n$ is an integer.
Some children considered what would happen if we changed the amount of consecutive numbers. Gajan from Wilson's School said:
When you add five consecutive numbers you get a multiple of 5. For example if you add 1+2+3+4+5 you get 15 which is a multiple of 5. It is interesting to note that when divided by 5 you will get the middle number in this case 3.
That is interesting, Gajan, and it's very similar to what happens when we add three consecutive numbers. I wonder if this works for other amounts of consecutive numbers as well?
Nikhil from Wilson's School explained why the pattern works for five consecutive numbers:
The total of an odd number of consecutive numbers is always the middle number multiplied by however many numbers are listed (midnumber x amountofnumbers).
If we have 1,2,3,4,5:
We have 5 numbers, and the middle number is 3, so the total must be 15. This is because the two numbers behind it are both the middle number -1 and -2, and the two numbers after it are both the middle number +1 and +2. These cancel each other out, so the list is essentially the same as 3,3,3,3,3.
Ronaldo from the British School of Paris in France sent in this picture to represent the -1 and -2 and the +1 and +2 that Nikhil mentioned:
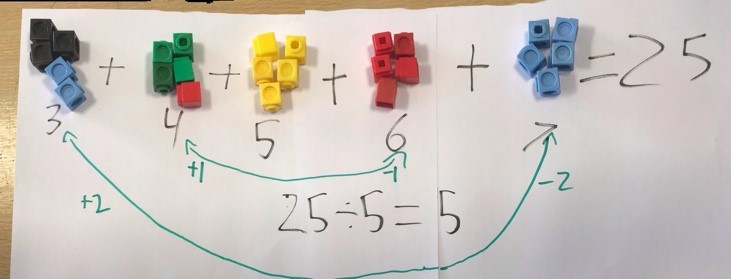
Well done to both of you for extending the reasoning from the case where there are three consecutive numbers. Take a look at Ronaldo's full solution to see the rest of his explanation.
Amélie from St Nicholas CE Primary School in England, Liam from Furness Academy in England and Tommy from New Cangle Primary School also sent in similar solutions for adding five and seven consecutive numbers together.
Roger from Westfield Academy in the UK, Olivia from Highgate School in the UK, Arnik, Aadit, Serena and Sunhari sent in algebraic solutions about adding five and seven consecutive numbers. This is Roger's work for five consecutive numbers:
When we add five consecutive numbers together, the sum is a multiple of 5. This can be proven algebraically as the five consecutive numbers can be represented algebraically as $n, n+1, n+2, n+3,$ and $n+4.$ Adding these terms together, and we get the formula to find the sum of the five consecutive numbers ($5n+10,$ where $n$ is the smallest number). Since the solution can be factorized by $5$ to result in $5(n+2),$ this proves that the sum of five consecutive numbers equals a multiple of $5.$
This is Serena's work for seven consecutive numbers:
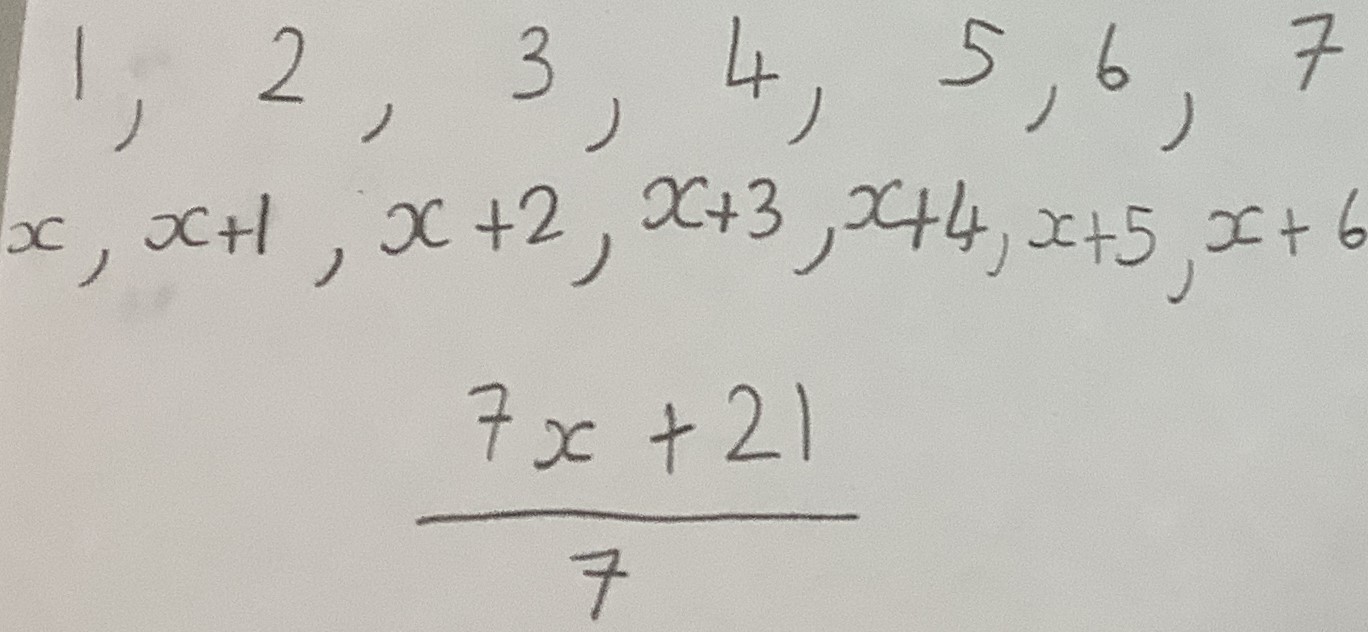
Aadit's proof for five consecutive numbers was slightly different, and Aadit claims that it works for any odd number of consecutive numbers:
If you try this with any amount of odd consecutive numbers [the sum] will be divisible by the amount of consecutive numbers.
For example, if it is $5$ consecutive numbers then those number will add up to a multiple of $5$ since if $n$ is the middle number again, the numbers will be: $n - 2, n - 1, n, n + 1$ and $n + 2.$
The $+2$ and $-2$ get cancelled out and the $+1$ and $-1$ get cancelled out. This leaves $5n$ so all you do is multiply the middle number by the amount of consecutive numbers (as long as that number is odd.)
Andy, Liam, Kai Yuan and Matthew sent in very similar work.
This is Sunhari's work about adding any odd number of consecutive numbers:
Sunhari's proof uses the formula $1+2+3+...+(n-)+n = \frac12n(n+1)$
I noticed that when the number of consecutive numbers is $(2k+1),$ and starting digit is $n,$ the sum of the consecutive numbers is $(2k+1)(n+k).$
Proof:
Suppose the numbers are: $n, n+1,…., n+(2k+1-1)$
$$\begin{split}n+n+1+n+2+…+n+2k & = n(2k+1) + (1+2+…+2k)\\ &=n(2k+1) + \tfrac122k(2k+1) \\&=
n(2k+1) + k(2k+1)\\&=(2k+1)(n+k)\end{split}$$
Milly and Skyrah from Drake Primary School in the UK investigated what happens when we add an even number of consecutive numbers:
When you add a multiple of three to another multiple of three, the end result is always a multiple of three. This works even when we have 5 consecutive numbers, 7 numbers, even 9 numbers! However, this only works with odd amounts of consecutive numbers. If I started to use even amounts, the result would start to change.
1 plus 2 is 3
2 plus 3 is 5
3 plus 4 is 7
Using just two consecutive numbers, it always ends up odd because an even number plus an odd number is always odd.
1 plus 2 is 3, 3 plus 4 is 7, so it ends up as 10
2 plus 3 is 5, 4 plus 5 is 9, so it ends up as 14.
3 plus 4 is 7, 5 plus 6 is 11, so it equals 18.
Four numbers means it's always an even number because adding two odd numbers always totals as an even number.
Liam investigated what happens when you add four consecutive numbers:
Kai Yuan and Matthew wrote a conjecture about any even number of consecutive numbers:
Conjecture with even numbers:
With even numbers, it is always a multiple of half the amount of even numbers, e.g. with 6 even numbers the total will always be a multiple of 3, as 3 is half of 6. Also, if $n$ is an even number, $n \div 2 (n + 1) =$ the first $n$ amount of consecutive numbers.
Evidence:
If you use the rainbow method of adding – e.g. $1 + 2 + 3 + 4 = 1 + 4 + 2 + 3 = 5 + 5 = 5 \times 2$ – you will find that you do $4 \div 2 (4 + 1) = 2 \times 5.$ This formula will always work with all even numbers.
Ci Hui Minh Ngoc from Kong Hwa in Singapore sent in an excellent investigation for adding 3 to 9 consecutive numbers, which makes use of Liz's method and Claire's method. Have a look at Ci Hui Minh Ngoc's work to see their reasoning. Shubhangee from Buckler's Mead Academy in England also investigated several different numbers of consecutive numbers:

Saanvi from Newcastle-under-Lyme Prep School in the UK used the idea of averages to explain what happens:
If you take three consecutive numbers (e.g. 3, 4 and 5) and add them together, you will always get a multiple of three. I think of it like this: if you take one away from the largest number and add one to the smallest number (5 - 1 = 4, 3 + 1 = 4 and 4 = 4) you are pretty much multiplying it by the middle number (4 + 4 + 4 = 4 x 3). You may also notice that this same pattern occurs when adding numbers with equal “distance” from each other (3, 6 and 9, for example), or you may notice that you are multiplying by the average of the three numbers. Using this knowledge, I worked out that you can relatively easily do this with any odd amount of consecutive numbers. For example, 1 + 2 + 3 + 4 + 5 = 3 x 5 = 15, or 7 + 8 + 9 + 10 + 11 = 9 x 5 = 45. Although this is slightly more complicated, you can do this with even amounts of numbers: 1 + 2 + 3 + 4 = 2.5 x 4 = 10. In this case 2.5 is the average and multiplying it by the amount of numbers (4) gets you to the total. Basically, to find out the total you must multiply the amount of numbers by the average of the numbers, which is true for any addition.
Well done, Saanvi! As well as thinking about consecutive numbers, Saanvi has extended this idea to other numbers that are equal 'distance' from each other. I wonder which average Saanvi is using in this explanation?
If you're interested in exploring different numbers of consecutive numbers in more detail, you may like to take a look at the task What Does it All Add up To?, which contains a proof sorter for four consecutive numbers for you to re-order.
Some children chose to investigate different patterns that they noticed when adding consecutive numbers. Unfortunately we don't have space to show every solution, but well done to the following children for noticing and giving excellent explanations for some very interesting patterns: Sion from Twyford School in England, Arabella from Highgate and Miraya from Heckmondwike Grammar School in the UK. Thank you all for sharing your ideas with us!
