 Links to the NRICH website Home page
Links to the NRICH website Home page

30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Round a Hexagon



- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
This activity proved to be a little tricky for many pupils so maybe some more thoughts need to be given about external and internal angles. What also made it harder was asking for some suggestions about proving the solution offered.
However, from Rebecca at the Baden Powell School in the UK we had this really good solution sent in.
If she went round every angle once when she went round the last angle she would be facing the way she started. She could also do this with a square or rectangle.
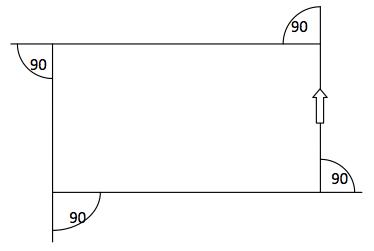
$90+90+90+90=360$
It also works with any triangle, because she always faces the same way when she gets back to the start.
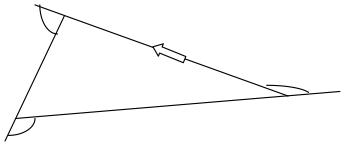
All shapes outer angles will add up to $360 °$ because Brenda always faces the same way when she gets back to the start.
From SooyoungӬ who said they went to GCMSӬ which I assume is Gosforth Central Middle School in the U.K.Ӭ we had the following interesting suggestion:
If you shrank the hexagon as small as a dot, the exterior angle would look like a rough circle which has 360 degrees altogether.
SophiaӬ at Towcester C E Primary School send in this thought of hers:
I think the answer is 360 degrees becuse the dot goes the whole way round and ended up facing the same way as it started. I added up $90, 90, 90$ and $90$ and it added up to $360$ degrees for a square a hexagon and a triangle.
So, thank you for those and I hope that there wil be even more learning about angles and shapes for us all.