 Links to the NRICH website Home page
Links to the NRICH website Home page

30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Walking Round a Triangle



- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
The questions asked were:
How much was turned?
Is it always the same and (the big question) - why?
There was a lot of confusion about the angles involved and most solutions that were sent in indicated $180$ degrees. This number of degrees is of course involved in what we know of triangles. However, when going around a triangle we do not turn the internal angle but $180$ minus the internal angle.
The solution sent in by a pupil from TNT school in Canada does quite well in showing this.
The triangle on which the ladybird walks has three arbitrary angles x, y, and z whose sum is $180$ degrees. The ladybird starts at S facing point A. Once it reaches A it turns an angle "a" and now faces point B. It does the same at point B and C (turning an angle "b" and face C;
turn an angle "c" and face A respectively). The sums of angles a and x, c and y, b and z are each $180$ degrees. By adding: $(a+x) + (y+c) + (z+b) =$ $540$ degrees and subtracting x,y and $z = 360$ degrees so the ladybird turns $360$ degrees.
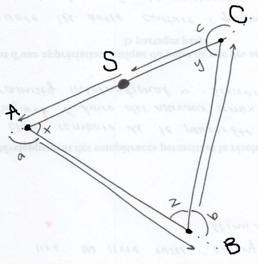
This would be the same for any triangle because this is a triangle with unspecified angles.
The other solution that tried to answer all the three questions was from Alexis who goes to Claremont Fan Court School, who goes on to say;
The Ladybird turns $360$ degrees in total. This is because in order to get back to the direction you were facing, you have to turn around $360$ degrees however many facings you go around. Ergo, this is true for any triangle, or any regular polygon for that matter.
Well done the two of you.